Konvergenzprobleme in progressiven Fehleranalysen
Beschreibung der gängigsten Probleme in den meisten progressiven Fehleranalysen
Die meisten handelsüblichen Finite-Element-Codes arbeiten mit Gleichungslösern auf Grundlage des Newton-Raphson-Algorithmus. Die im Newton-Raphson-Algorithmus implizite grundlegende Annahme ist, dass die nichtlineare Reaktion des Systems ausreichend gleichmäßig verläuft. Wenn die nichtlineare Reaktion des Systems gleichmäßig genug ist und der Newton-Raphson-Algorithmus mit einer angenäherten Lösung eingeleitet wird, die ausreichend nahe an der tatsächlichen liegt, produziert der Newton-Raphson-Algorithmus eine Reihe von Lösungen mit quadratischer Konvergenz (siehe qualitative Illustration in Teil A der Grafik unten).
In einer progressiven Fehleranalyse ist die nichtlineare Reaktion des Systems jedoch nicht gleichmäßig, besonders nicht auf der lokalen Ebene, wo Materialfehler zu großen Unterbrechungen im Konstituentenverhalten des Materials führen (siehe z. B. die Grafik im Abschnitt Schadenszustände in unidirektionalen Verbundmaterialien). Die ungleichmäßige Reaktion des Systems ändert die Konvergenzmerkmale des nichtlinearen Lösungsvorgangs vollständig. Teil B der Abbildung unten bietet eine qualitative Veranschaulichung des Typs von Konvergenzverhalten, der bei der Lösung ungleichmäßiger Systeme wie jenes in progressiven Fehleranalysen auftritt. Das wichtigste in Teil B beobachtete Merkmal ist die Tatsache, dass im Verlauf der Gleichgewichtsiterationen die größte Restkraft nicht unbedingt eine kontinuierliche Abnahme aufweisen muss. Im Gegenteil: Die größte Restkraft bleibt relativ konstant, bis alle Restkräfte plötzlich verschwinden, was darauf hinweist, dass die Lösung gefunden wurde.
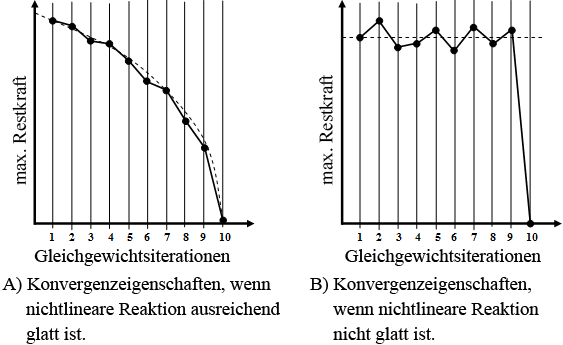
Die nichtlineare Lösungsstrategie der meisten handelsüblichen Finite-Element-Codes basiert auf der Annahme, dass das System die Konvergenzmerkmale aus Teil A oben aufweist. Genauer gesagt gehen handelsübliche FE-Codes davon aus, dass die größte Restkraft im Zuge der Gleichgewichtsiterationen kontinuierlich und schnell abnimmt. In dem Fall, dass Restkräfte mit jeder neuen Gleichgewichtsiteration keine offensichtliche Abnahme aufweisen, nehmen kommerzielle FE-Codes an, dass die Menge an Nichtlinearität im aktuellen Zeitschritt einfach zu groß ist. Daher wird die Größe des Zeitschritts reduziert, um zu versuchen, die Menge an Nichtlinearität in der Systemreaktion zu verringern. Dieser Ansatz ist für die progressive Fehleranalyse nicht geeignet, da die nichtlineare Systemreaktion nicht gleichmäßig verläuft und nicht davon ausgegangen werden kann, dass die Restkräfte kontinuierlich abnehmen. Die Anwendung dieser Methode auf die progressive Fehleranalyse ist sogar kontraproduktiv, da sie zu extrem kleinen Zeitschritten führt, die für den Abschluss der Analyse nicht geeignet sind.
Firehole Composites (jetzt Autodesk) hat eigene Algorithmen entwickelt, die in Helius PFA integriert wurden, um die bei einem schnellen Zerfall der Materialsteifheit häufig auftretenden Konvergenzprobleme zu lösen. Wenn Helius PFA für den Zerfall der Materialsteifheit verwendet wird, bietet der Finite-Element-Code eine robuste Konvergenz für die progressive Fehlersimulationen. Ausgehend von umfangreicher Erfahrung mit progressiven Fehleranalysen wird empfohlen, dass der Finite-Element-Code mindestens 50 Gleichgewichtsiterationen zulassen soll, bevor eine Verringerung der Lastinkremente angedacht wird.