Fiber Constituent Failure Criterion
The assumptions that follow are used in developing the fiber constituent failure criterion.
Fiber failure is assumed to be influenced by the fiber average stress components
, 
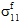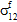, and 
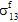.Fiber failure is assumed to be independent of the fiber average stress components
, 
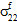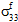, and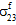 
.The contribution of
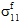in producing fiber failure depends upon whether 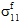is tensile or compressive.The fiber constituent is assumed to be transversely isotropic; consequently, you cannot distinguish between the contributions of
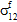and 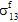to fiber failure.In unidirectional composites, the fiber constituent is considered to be a transversely isotropic material; however, fiber failure is assumed to be an isotropic event. In other words, regardless of the particular mix of stress components responsible for producing fiber failure, the effect of fiber failure on the stiffness of the fiber constituent remains the same. Specifically, when fiber failure occurs, each of the fiber average moduli (
, 
, 
, 
, 
, 
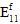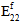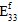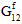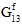) are reduced to a user-defined percentage of their original values (the default is 1%), while the fiber average Poisson ratios (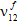
, 
, 
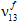) are assumed to remain unchanged.Note: This stiffness reduction scheme implies that, regardless of the combination of stress components that cause fiber failure, there is only one fiber failure mode and it results in a uniform degradation of all fiber moduli.In woven composites, fiber failure is assumed to be an orthotropic event; specifically,
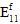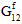, , and 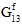are degraded, while 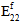, , 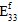and remain unchanged.
Using these five basic assumptions, researchers from the University of Wyoming and Autodesk have developed the following fiber failure criterion that is expressed as a quadratic function of the fiber average stress components.
The quantities 
(i = 1,4) are two of the transversely isotropic invariants of the fiber average stress state.
The quantities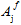 
(j = 1,4) are the adjustable coefficients of the fiber failure criteria. In Eq. 26, if a superscript symbol '±' precedes the coefficient 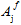, it indicates that the value of depends on whether the associated fiber average stresses are tensile or compressive; hence 
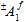represents two possible values. Therefore, the fiber failure criterion (Eq. 26) contains a total of three adjustable coefficients that must be determined using measured strengths of the composite material.
It is worth noting that the fiber average stress components that make up the invariants are total stress terms. That is, they encompass both mechanical and thermal stresses. When thermal residual stress calculations are activated, the residual stresses in the fiber constituent that result from the post-cure cooling of the material are explicitly included in the total stress -- prior to any externally applied mechanical or thermal loads. These residual stresses are caused by differences in the coefficients of thermal expansion of the fiber and matrix constituents. Typically, during post-cure cooling of the composite, the matrix constituent attempts to shrink more than the fiber constituent. Thus, the matrix constituent exhibits tensile thermal residual stresses and the fiber constituent exhibits compressive residual stresses. Refer to the Thermal Residual Stresses topic for a description about how these thermal residual stresses are determined.
Collectively, the matrix and fiber constituent failure criteria contain a total of 13 adjustable coefficients for unidirectional composites and six adjustable coefficients for woven composites. The procedure for determining values for these coefficients is described later (Failure Criteria for Unidirectional Composites).