Numerical Form of the MCT Decomposition

View the numerical decomposition based on the use of finite element models of the composite material.

Composite materials are often more complex than a simple unidirectional fiber reinforced material that contains only fiber and a matrix constituents. For example, woven and braided composites contain a meso-structure composed of two or more families of tows and pure matrix pockets (i.e., meso-constituents). The tow meso-constituents are composed of micro-constituents (fiber and matrix). In this case, the woven composite average stress and strain states must be decomposed into the appropriate meso-constituent average stress and strain states. Then the meso-constituent average stress and strain states must be further decomposed into micro-constituent (fiber and matrix) average stress and strain states. Helius PFA performs the final decomposition using the analytical binary decomposition described earlier (Analytical Form of the MCT Decomposition). However, the analytical binary decomposition is not practical for performing the first decomposition (from composite average values to meso-constituent values) because there are more than two meso-constituents. Also, in the case of a composite material that contains more than two micro-constituents, the analytical binary decomposition is not practical. For decompositions to three or more meso-constituents or micro-constituents, Helius PFA uses a numerical decomposition based on the use of finite element models of the meso-structure or micro-structure of the composite material.

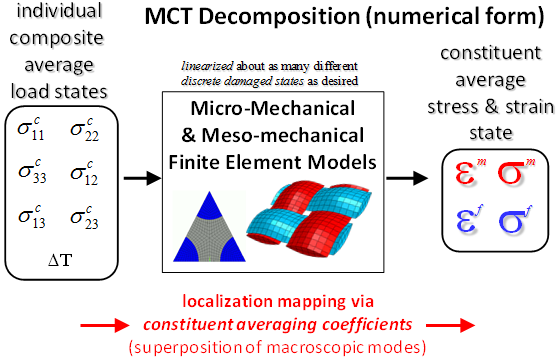
The picture below shows a schematic diagram of the numerical decomposition method which relies on high fidelity finite element models of the composite material's meso-structure and micro-structure. For example, for a plain weave composite, the numerical method would require the use of a meso-scale finite element model of the woven composite that used a homogenized material description of the warp tows, fill tows and matrix pockets, i.e., a finite element model with three meso-constituents. Individual homogeneous macroscopic stress states can be imposed on the meso-scale finite element model, and the resulting solution can be used to compute the average stress and strain states in the homogenized warp tows, homogenized fill tows, and pure matrix pockets. These meso-scale finite element solutions can be used to compute sets of influence coefficients that directly map macroscopic stress and strain components into meso-constituent average stress and strain states for the warp tows, fill tows, and matrix pockets. A set of these meso-constituent influence coefficients are determined for each discrete damage state that can be exhibited by the woven composite material. The resulting coefficients are stored in a material database for immediate access during a structural-level progressive failure simulation. Finally, the average stress and strain states in the homogenized warp tows and fill tows can be decomposed into fiber and matrix average stress and strain states using the analytical binary decomposition.