Analysis Characteristics

• Steady-state
• Three Dimensional Internal Flow
• Turbulent
• Incompressible Flow
• Distributed Resistance Models

Reference

White, F.M., “Fluid Mechanics”, McGraw-Hill, New York, 1979, pp. 305-360

Idelchik, I.E., “Handbook of Hydraulic Resistance”, CRC Press, 1994, pp. 523

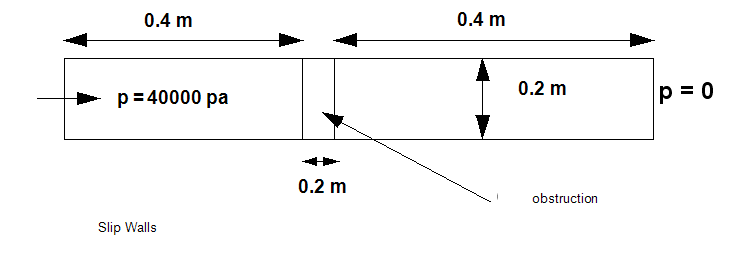
Problem Description

Air flows through a 3D channel with slip walls with a filter (or some flow obstruction) in the center of the channel. The pressure drop across the channel is due to only the obstruction because the walls have slip conditions.

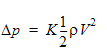
All 4 distributed resistance models are tested:

1. Constant K factor:

K = 1.97748

At the specified pressure drop, this K factor should result in a flow rate of 0.2 m3/s.

2. Pipe friction loss:

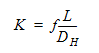
where 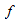is the friction factor for which we use a Blasius formula for the friction factor. L = 41.99 is the pipe length to be represented, and DH = 0.2 is hydraulic diameter of the pipe. The Blasius formula used to determine the friction factor is:

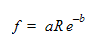
where a is 0.316 and b is 0.25. These values should result in an equivalent K-factor value of 1.97748. Hence, we can expect a flow rate 0.2 m³/s.

3. Free area ratio

For this resistance type, we use the formula from page 516 in Idelchik:

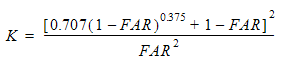
where FAR is the free area ratio. For a free area ratio of 0.62, we get a K factor of 1.9774 and thus a flow rate of 0.2 m³/s.

4. Head-loss table K factor:

We use the following table of values:

Flow Rate (m3/sec)	Pressure Head (Pa)
0.15	35000
0.25	45000

Geometry and Boundary Conditions

Results

Distributed Resistance Type	Benchmark	2018: Build 20170308	% Error	2019: Build 20180130	% Error
Constant K	0.2 m3/s	0.1997	0.143	0.1961	1.95
Pipe Friction Loss	0.2 m3/s	0.2171	8.569	0.1982	.896
Free Area Ratio	0.2 m3/s	0.1997	0.143	0.1961	1.95
Head Loss Table	0.2 m3/s	0.1979	1.0475	0.1999	.004