Designaciones adoptadas:
E: módulo de Young
G: módulo de Kirchoff
ν: coeficiente de Poisson
fd: límite de elasticidad
Ax: área de sección transversal
Ix: constante de torsión
Iy: momento de inercia; flexión en el plano XZ
Iz: momento de inercia; flexión en el plano YZ
ky, kz: coeficientes de corrección de resistencia al cortante en las direcciones Y y Z
L: longitud de la barra
-
Comentarios preliminares e hipótesis
Se utilizan las siguientes hipótesis para los elementos de barra (viga):
- Formulación uniforme para 2D y 3D (pórticos 2D y 3D, emparrillados)
- Elemento uniforme que permite la no linealidad geométrica o del material
- Grados de libertad de desplazamiento estándar en 2 nudos extremos
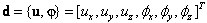
- Se permite el uso de los siguientes elementos:
- Deformación cortante incluida (modelo de Timoshenko).
- Sección transversal cónica: solo para no linealidad geométrica.
- Tierra de Winkler.
- Existen dos niveles de no linealidad geométrica disponibles: P-Delta (teoría de segundo orden) y Desplazamientos grandes, que es la teoría más precisa posible con desplazamientos y rotaciones grandes; este es un enfoque incremental con una actualización de la geometría.
- Si se supone que hay pequeños desplazamientos y ausencia de no linealidad física para el límite, los resultados son idénticos a los de los elementos lineales estándar.
- En el análisis de no linealidad del material, se aplican el modelo en capas y el principio de tensión-deformación constitutivo para la tensión-deformación uniaxial en el nivel de punto (capa).
- Los estados de cortante y torsión se tratan como elásticos lineales y deben desacoplarse de fuerzas axiales y momentos flectores en el nivel de sección transversal.
- Las rótulas y las relajaciones no lineales solo se pueden definir como elementos DSC.
- Se admiten todos los tipos de cargas de elementos (igual que para los elementos estándar). Sin embargo, se supone que las fuerzas nodales que actúan sobre una estructura se determinan al principio del proceso. Los cambios en la transferencia de cargas de elementos a nudos resultantes de la no linealidad geométrica o del material se ignoran.
- Además del elemento elastoplástico, también es posible generar rótulas elastoplásticas en las secciones transversales de la barra seleccionadas como extensión de la opción "rótulas no lineales" (véase el punto 5).
-
Aproximación a la geometría, la cinemática y las deformaciones
Convención de signos de geometría para fuerzas, desplazamientos, tensiones y deformaciones
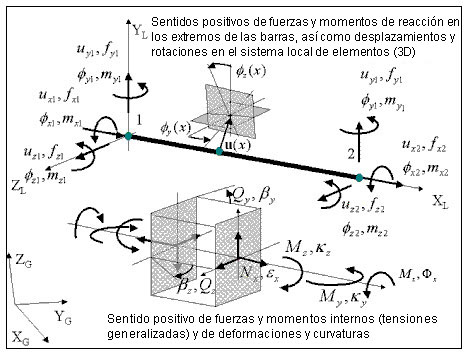
Relaciones cinemáticas básicas
En el sistema local del elemento y en el rango geométricamente lineal, las deformaciones generalizadas E en el nivel de sección transversal son las siguientes (el símbolo
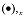indica el cálculo del diferencial a lo largo de la dirección del eje de la barra):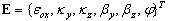 
donde:
Deformación axial en el eje de la barra:
e0x = u ,x
Curvaturas:
K y = fy'x
K z = - f z'x
Ángulos medios (deformación):
b y = n 'x - f z'
b y = w 'x - f y
Ángulo de torsión unitaria:
j = f x'x
Aproximación al desplazamiento
Cuando existe la posibilidad de considerar la influencia cortante y la coherencia de los resultados obtenidos para el elemento lineal, se han implementado funciones de forma física que tienen en cuenta la influencia de cizalla.
Barras 2D:
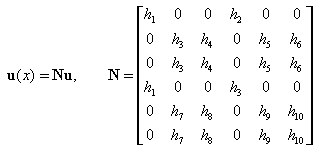
Las fórmulas expresan las funciones de forma y sus derivadas:
donde:
x = x / L
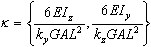para los planos XY y XZ, respectivamente. Relaciones cinemáticas para la notación de matriz (teoría geométricamente lineal)
Al tener en cuenta la influencia de las deformaciones impuestas
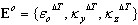
Incremento de deformaciones generalizadas (en sección):
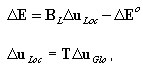
2D:
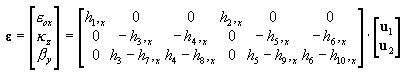
3D:
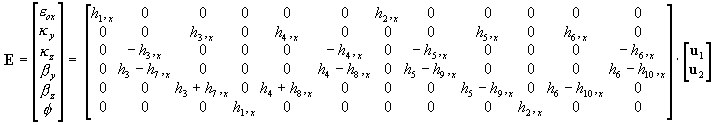
donde:
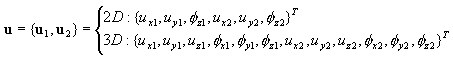
Deformaciones en un punto (capa)
Si se especifican las deformaciones generalizadas {ε 0x, k y , k x } de una sección transversal, la deformación e xl o su incremento De xl en cualquier punto de la sección transversal l - de las coordenadas yl, zl, se calcula como se indica a continuación:
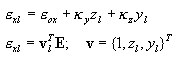
Por último, el incremento de deformación en la capa:
-
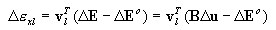
Tensiones y fuerzas internas en un elemento
El principio constitutivo en el nivel de puntos
El principio se adopta en forma incremental general, donde las tensiones actuales σx n+1 se definen como una función de la tensión del último equilibrio σx n y el incremento de tensión actual teniendo en cuenta las deformaciones (térmicas) impuestas, como se indica a continuación:
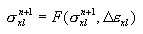
Según la función σ = f(ε) que describe la relación en el proceso de carga activa y en la especificación del principio de descarga y recarga. En concreto, puede ser el principio elastoplástico con endurecimiento lineal y el principio especificado de descarga, como (a) elástico, (b) plástico, (c) daño o (d) mixto. Para la descarga elástica, el proceso pasivo y activo se realiza a lo largo de la misma ruta σ = f(ε). Para los demás, se realiza a lo largo de la línea recta determinada por el punto inicial de un proceso de descarga determinado {ε UNL, σ UNL } y el módulo de descarga D UNL , que se define de la siguiente forma:
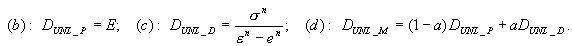
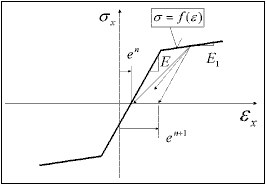
e n es una deformación memorizada, para la que se ha iniciado el proceso activo actual, iniciado tras superar 0 por tensiones con la descarga (e 1 = 0) asumida.
Para el análisis, es necesario proporcionar la rigidez actual, que se presupone que es una derivada:
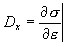
Cálculo de fuerzas y valores de rigidez de la sección transversal.
En el nivel de sección transversal, el vector de los esfuerzos internos (resultados de tensiones) se compone de lo siguiente:
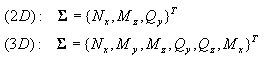
Los estados de cortante y torsión ΣST se tratan como elásticos lineales y no se conjugan con el estado de las fuerzas axiales/de flexión en el nivel de sección transversal.
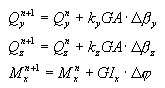
Los estados de compresión/tensión Σ NM se tratan normalmente como conjugados al aplicar el método por capas. Sin embargo, siempre que el estado elástico esté garantizado, por ejemplo, hasta que las deformaciones generalizadas actuales cumplan la siguiente condición de estado elástico:
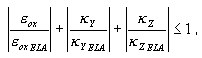
donde:
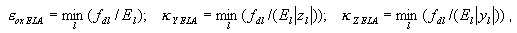
La sección transversal se trata como elástica y el método por capas no está activado.
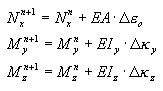
Una vez que se afirma la infracción de la condición de estado elástico, las tensiones inducidas por las deformaciones axiales y la flexión se calculan por separado para cada capa y sobre su base se calculan las cantidades seccionales.
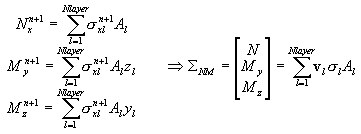
La rigidez en el nivel de la sección transversal D se calcula de la siguiente manera:
En estado elástico como se indica a continuación:
D = diag {EA, EIy, EIz, KyGA, kzGA, GIx)
Después de superar la condición de estado elástico, como se indica a continuación:
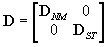
donde:
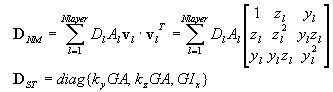
Matriz de rigidez del elemento y vector de fuerza nodal
Se calculan mediante las fórmulas estándar que aplican la cuadratura de Gauss (Ngauss=3).
-
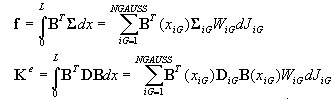
No linealidad geométrica
Se tienen en cuenta las siguientes configuraciones:
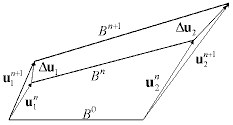
B0: configuración inicial
Bn: configuración de referencia (la última para la que se cumplen las condiciones de equilibrio)
Bn+1: configuración actual (iterada)
Un punto de entrada para la formulación del elemento es el principio de trabajo virtual guardado de la siguiente forma para los incrementos de desplazamiento:
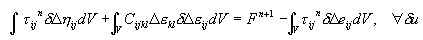
donde el aumento de la deformación Δε mientras se mueve Bn a Bn+1, Δe, Δη constituye sus partes de la forma correspondiente, lineal y no lineal con respecto al incremento de desplazamiento Δu, mientras que τ es una deformación que se refiere a la configuración de referencia y Cijkl es un tensor de módulos de elasticidad tangencial.
La opción de no linealidad
Se corresponde con la formulación no lineal o la teoría de segundo orden. Como es posible la no linealidad del material, se introduce la formulación incremental (aunque sin modificar la geometría del elemento).
Relaciones cinemáticas
Incrementos de deformación en la notación de matriz:
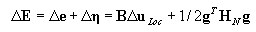
donde:
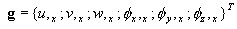
A continuación, el gradiente de incremento de desplazamiento g = ΓΔu
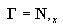
considerando que
es una matriz de selección.
Matriz de rigidez del elemento y vector de fuerza nodal
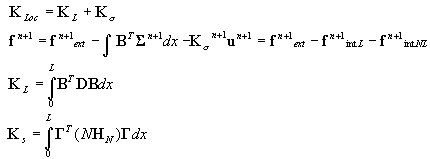
Algoritmo en el nivel de elemento
La geometría del elemento no se modifica; la transformación local-global se realiza con el uso de la matriz de transformación inicial 0T.
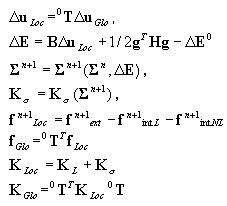
Opción de desplazamiento grande
Es una determinada variante de la descripción de barra que permite desplazamientos grandes. El método de la descripción de Lagrange actualizada se aplica aquí.
Matriz de rigidez del elemento y vector de fuerza nodal
-
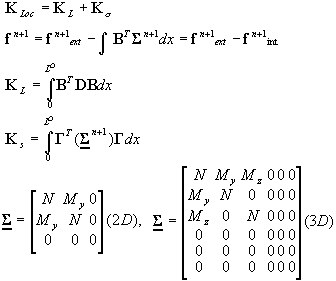
Rótulas elastoplásticas
También se puede modelar el trabajo elastoplástico de una estructura mediante la introducción de rótulas no lineales en las secciones transversales de barra seleccionadas. Las características de una rótula representada por un elemento DSC de dos nudos se definen mediante la aplicación del algoritmo de análisis de sección transversal descrito en el punto 3, suponiendo que la función de deformaciones generalizadas E se lleve a cabo mediante desplazamientos de nudo mutuos (con respecto a las direcciones locales de las barras) divididos por la longitud de elemento (ficticia) adoptada (ΔL) que equivale a la altura mínima de la sección transversal. Estos actúan como el volumen de elemento dV=ΔL. Las fuerzas y los desplazamientos de los nudos recién generados del elemento DSC constituyen un nivel global de libertad, es decir, no se someten a condensación.
Algoritmo en el nivel de elemento-
Cálculo de deformaciones generalizadas en una sección transversal
-
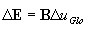
Cálculo de los esfuerzos internos (resultantes de las tensiones) y la rigidez de la sección transversal según el punto 3.2
-
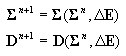
Cálculo de fuerzas (reacciones en los extremos de las barras) y rigidez del elemento DSC
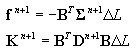
donde:
-
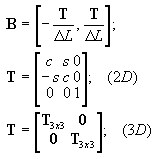