Un análisis no lineal consiste en la aplicación incremental de cargas. Durante los cálculos, las cargas no se tienen en cuenta en un momento específico, sino que se incrementan gradualmente y se aplican soluciones a los sucesivos estados de equilibrio.
El comportamiento no lineal de una estructura puede deberse a un único elemento de estructura (no linealidad estructural o de material) o a una relación fuerza-deformación no lineal en toda la estructura (no linealidad geométrica).
Los siguientes elementos no lineales pueden provocar una no linealidad estructural:
- Elementos de compresión/tensión
- Elementos de cables
- Restricciones no lineales (es decir, restricciones o apoyos unilaterales, relajaciones, nudos compatibles con el parámetro de rigidez asignado)
- Plastificación del material
- Rótulas no lineales
Opciones de no linealidad geométrica
Las opciones de no linealidad geométrica tienen en cuenta los efectos reales de orden superior y a menudo mejoran la convergencia del proceso de cálculo en una estructura que incluye elementos no lineales.
- Análisis P-Delta
- Este análisis tiene en cuenta los efectos de segundo orden, como el cambio de la rigidez del elemento bajo la influencia del estado de tensión en el elemento. También tiene en cuenta la generación de momentos resultantes de la acción de fuerzas verticales en los nudos desplazados horizontalmente.
- Análisis de desplazamientos grandes
- Este análisis tiene en cuenta los efectos de tercer orden, como la rigidez lateral adicional y las tensiones resultantes de la deformación o la rotación. Este efecto tiene en cuenta las fuerzas adicionales que surgen en una estructura deformada. Por ejemplo, en una viga con apoyos fijos en ambos extremos y con una carga vertical, se generan fuerzas longitudinales y la deflexión disminuye.
Estos parámetros de análisis pueden mejorar la convergencia del proceso de cálculo, ya que tienen en cuenta los efectos reales de orden superior. Esto resulta especialmente útil cuando se trabaja con una estructura que incluye elementos no lineales.
Se pueden utilizar dos métodos para resolver un sistema de ecuaciones no lineales: el método incremental y el método de longitud de arco.
Método incremental
Si una estructura incluye elementos no lineales (como cables, apoyos unilaterales y plasticidad de materiales), se realizan cálculos que aplican el método incremental.
Con el método incremental, el vector de carga de la derecha se divide en n incrementos iguales. Una vez alcanzado el estado de equilibrio del incremento anterior, se aplica un incremento de carga consecutivo a la estructura. Se especifica la norma de fuerzas desequilibradas para cada paso, lo que permite supervisar las relaciones fuerza-deformación de la estructura.
La figura siguiente muestra un ejemplo de un proceso no lineal que utiliza el proceso incremental. Se muestran los valores utilizados para los cálculos no lineales.
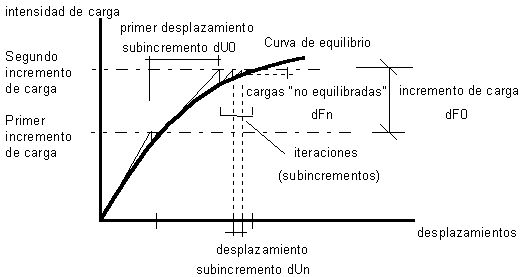
El incremento de carga se utiliza al dividir una carga en segmentos más pequeños. En el caso de estructuras complejas en las que el impacto de los efectos no lineales es considerable, es posible que los cálculos no converjan si el análisis del valor de una carga se aplica en un solo paso. El número de incrementos de carga influye en el número de iteraciones de cálculo. Cuanto mayor sea el número de incrementos, mayor será la probabilidad de que los cálculos alcancen el punto de convergencia.
Método de longitud de arco
Se debe aplicar el método de longitud de arco en la conducción de desplazamiento cuando los algoritmos incrementales de resolución de ecuaciones mediante conducción por fuerza no sean convergentes.
El método de longitud de arco se aplica durante el análisis de deterioro no lineal. Se recomienda encarecidamente cuando se definen atributos de estructura no lineal en un modelo de estructura (véase el apéndice).
Proceso de análisis
- Método de tensión inicial.
- Método de Newton-Raphson modificado.
- Método completo de Newton-Raphson.
En general, el método de tensión inicial es el más rápido y el método completo de Newton-Raphson es el más lento. Sin embargo, la probabilidad de convergencia es mayor con el método completo de Newton-Raphson que con el método de tensión inicial.
En la siguiente tabla se muestra cómo definir las opciones de actualización de la matriz para utilizar el algoritmo adecuado.
| Algoritmo | Actualización de la matriz después de cada subdivisión | Actualización de la matriz después de cada iteración |
|---|---|---|
| Tensión inicial | Desactivada | Desactivada |
| Newton-Raphson modificado | Activada | Desactivada |
| Newton-Raphson completo | Activada | Activada |
El algoritmo del procedimiento Broyden-Fletcher-Goldforb-Shanno (BFGS) modifica la matriz de rigidez durante los cálculos. En algunos casos, el uso del algoritmo de búsqueda de líneas puede mejorar la convergencia del método.
Cuando se alcanza el estado de equilibrio, el proceso de iteración se detiene y se comprueba la convergencia del proceso. Los incrementos de desplazamiento dUn y las fuerzas desequilibradas dFn son básicamente cero o un valor suficientemente pequeño en comparación con los parámetros de tolerancia de ambos valores. El proceso de iteración se detiene si se produce una divergencia. La falta de convergencia puede interpretarse como el efecto numérico de las sobrecargas de la estructura o como resultado de una inestabilidad numérica del proceso, como cuando la carga se divide en un número reducido de intervalos. En tales casos, se puede aumentar el número de incrementos de carga, lo que suele contribuir a que se produzca la convergencia en el proceso.
Consulte también:
Elementos de barra en el análisis no lineal disponible en Robot