El algoritmo para las flechas de losas de hormigón armado se basa en el uso de cálculos de losas elásticas isotrópicas compuestas de material elástico. Se tienen en cuenta los cambios de rigidez del material debidos a la fisuración. Los desplazamientos se calculan mediante la aplicación del método de elementos finitos (MEF) y, a continuación, se modifican.
Los cálculos se realizan por separado para cada panel. Este supuesto es correcto si se puede identificar un panel con un elemento estructural (segmento de suelo o tramo); de lo contrario, los valores de rigidez promediados en un panel pueden estar distorsionados. Esto puede provocar la influencia de elementos muy distantes en los desplazamientos de un EF analizado. La influencia de estas perturbaciones en valores extremos no es muy significativa. Sin embargo, los mapas de deformaciones (flechas) deberían utilizarse con gran cuidado.
Es recomendable modelar cada segmento de suelo en el que se pueden producir extremos locales de flechas como un panel independiente. Este panel debe definirse dentro de los límites establecidos por los apoyos que lo rodean (de forma similar a los tramos que están limitados por apoyos en el caso de las vigas). Para un panel, estos apoyos no tienen que ser continuos en todo el contorno del panel.
La división en paneles no afecta a los resultados de la verificación mediante el método de actualización de rigidez (MEF) siempre que las cargas, la geometría y la armadura calculadas sean iguales.
Los cálculos se realizan para una combinación seleccionada (independiente para los desplazamientos inferior y superior) o un grupo de combinaciones, si así lo requiere la norma (combinaciones frecuentes, poco frecuentes y cuasipermanentes). Esta combinación se selecciona para los cálculos en los que hay desplazamientos elásticos máximos (positivos y negativos por separado). Si un panel no se puede tratar como un elemento estructural (contiene más elementos de estructura), los mapas de deformaciones (flechas) deben utilizarse con extremo cuidado. Sin embargo, no tiene ninguna influencia significativa en los valores de flechas extremas de un panel especificado.
Se debe prestar atención a los desplazamientos de las esquinas de apoyo restantes de una losa.
El algoritmo de cálculo utilizado en el programa Robot se basa en el supuesto de que las flechas totales (reales) de una losa de hormigón armado equivalen al producto de sus flechas elásticas y el coeficiente de rigidez D / B.
donde:
: desplazamientos reales del punto de cálculo en la posición i de una losa, teniendo en cuenta la fisuración y la armadura calculada.
: desplazamientos elásticos del punto de cálculo en la posición i de una losa.
D: rigidez de la losa presuponiendo la elasticidad del material (como en los cálculos de MEF).
B: rigidez equivalente de una losa de hormigón armado, calculada teniendo en cuenta la fisuración de elementos, los efectos reológicos y la adherencia de la armadura calculada, entre otros elementos, y promediada para ambas direcciones.
Este enfoque se reduce a la escala lineal de los desplazamientos elásticos individuales mediante el coeficiente global de reducción de la rigidez.
El algoritmo de cálculo para el método de rigidez equivalente (elástico) es el siguiente:
Después de realizar el análisis de la estructura mediante MEF y calcular el área de armadura necesaria para el estado límite definitivo, el estado límite de servicio (en lo que respecta a los cálculos de fisuración, los límites de tensión u otros problemas que se pueden tener en cuenta localmente) y el estado límite accidental, la rigidez de cada elemento finito (EF) se evalúa en el programa. Los cálculos de rigidez se realizan en dos direcciones de la armadura. El ámbito y el método de cálculo de estos valores de rigidez dependen de los requisitos detallados de una determinada norma. Como resultado de estos cálculos, se obtienen dos valores de rigidez (diferentes en la mayoría de los casos) para cada elemento finito. Para realizar cálculos adicionales, se utiliza una media ponderada de los valores de rigidez del componente. El peso de la media es la relación de los momentos que actúan sobre un elemento especificado en ambas direcciones.
donde:
Bx, By: valores de rigidez reales calculados para dos direcciones de la armadura
cf: coeficiente de peso calculado según la fórmula
- Si | Mxx | / | Myy | > 4, cf = 1.
- Si 0.25 ≤ | Mxx | / | Myy | ≤ 4,
.
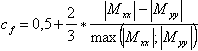- Si | Mxx | / | Myy | < 0.25, cf = 0.
Como resultado de la aplicación de estas fórmulas, en el caso de una gran desproporción de los momentos (la relación entre el momento mayor y el menor es superior o igual a 4.0), se tiene en cuenta la rigidez desde la dirección de la acción del mayor de los momentos. Cuando los valores de los momentos son similares, el espesor de una dirección determinada se asigna en proporción a la relación de los momentos.
El siguiente paso es evaluar la relación entre la rigidez elástica y la media ponderada de los valores de rigidez reales obtenidos como se ha mencionado anteriormente. Este cálculo se realiza para cada elemento finito.
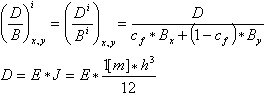
El coeficiente de la losa (1 - n*n) se tiene en cuenta en los cálculos de la rigidez B y D.
Los valores de rigidez reales obtenidos en los cálculos se pueden ver mediante la activación de los mapas del factor de rigidez.
Si las propiedades de los materiales utilizados durante el diseño son idénticas a las utilizadas en un modelo, el valor del coeficiente D / B es superior a 1.0. Este coeficiente se puede interpretar (principalmente para losas sometidas a flexión unidireccional) como un multiplicador de flecha elástica. Si se utilizan materiales diferentes en un modelo y los cálculos (por ejemplo, con clases distintas, como hormigón con un módulo de Young o coeficiente de Poisson diferentes), el valor del coeficiente se corrige automáticamente. Esto puede provocar perturbaciones en la desigualdad mencionada anteriormente.
El paso siguiente consiste en calcular la media de los coeficientes de rigidez evaluados anteriormente. El coeficiente de rigidez global final, utilizado para el cálculo de los desplazamientos reales de una losa (como la escala lineal de los desplazamientos elásticos) es un promedio de los coeficientes de rigidez media (con un peso igual a 0.25) y el coeficiente de rigidez registrado para un elemento en el que existe el extremo del momento flector que actúa en cualquier dirección (con un peso igual a 0.75).
El algoritmo del método de rigidez equivalente (elástico) presupone la media de rigidez de todos los elementos finitos; por lo tanto, una forma de la línea de flecha es idéntica a la línea de flecha multiplicada por el coeficiente de rigidez.
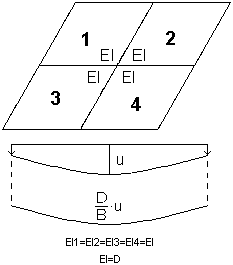
El algoritmo del método con actualización de rigidez (inelástico) es idéntico al algoritmo del método de rigidez equivalente (elástico) hasta que la rigidez calculada se asigna independientemente a cada elemento finito (rigidez diferente para la dirección X y la Y). Se obtiene una losa anisotrópica con diversos grados de rigidez. Para los valores de rigidez determinados por esta opción, se calcula la flecha de losa.
En el método con actualización de rigidez, la rigidez de cada elemento se calcula de forma independiente, por lo que las líneas de flecha pueden diferir. Se obtiene una rigidez diferente para cada elemento finito en cada dirección.
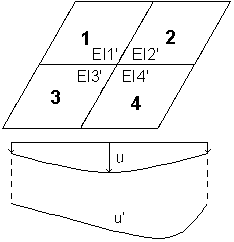
Si la opción Corrección de armaduras está seleccionada en la ficha Parámetros ELS del cuadro de diálogo Parámetros de armadura de losa y lámina durante los cálculos, el área de armadura aumenta (para incrementar la rigidez del elemento), lo que reduce las flechas de losa.
Las armaduras en ambas direcciones se distribuyen en proporción inversa a la rigidez. Cuando no se puedan limitar las flechas por debajo del valor de flecha admisible definido por el usuario (cuando es imposible corregir de forma adicional la armadura debido al grado de armadura admisible), si se completan los cálculos del área de armadura necesaria, un aviso indica que se ha superado el valor de flecha admisible para el panel.
No hay límites predefinidos establecidos en la armadura, excepto los de las normas. Observe el aspecto económico de la solución proporcionada; cuanto más difiera una flecha de los requisitos, menos eficaz será el método utilizado.