Pour sélectionner les paramètres de simulation dynamique

Une fois modifiées, ces options s'appliquent à la simulation dynamique jusqu'à ce que vous les modifiiez à nouveau. Dès que vous avez ouvert l'application Simulation dynamique, définissez immédiatement les options.

1. Sur le ruban, cliquez sur l'onglet Environnements le groupe de fonctions Commencer... Simulation dynamique pour afficher les panneaux de simulation dynamique.
2. Cliquez ensuite sur l'onglet Simulation dynamique le groupe de fonctions Gérer Simulation Settings .
3. Cliquez sur Convertir automatiquement les contraintes en liaisons standard afin d'activer le convertisseur de simulation dynamique (ou moteur de réduction des contraintes).

   Par défaut, il est activé.

   Lorsque vous cliquez sur OK, le moteur de réduction des contraintes convertit automatiquement les contraintes d'ensemble en liaisons standard, puis met à jour les liaisons converties lorsque vous ouvrez le mécanisme par la suite.

4. Si vous souhaitez être averti d'une sur-contrainte de mécanisme, cliquez sur Avertir en cas de mécanisme surcontraint.

   Cette option est définie par défaut pour les nouveaux mécanismes, mais pas pour les mécanismes créés avant la version 2008. Lorsqu'elle est activée, si le mécanisme est surcontraint, le logiciel affiche un message après que vous avez cliqué sur OK et avant de créer automatiquement les liaisons standard.

5. Si vous souhaitez avoir une indication visuelle des composants inclus dans les divers groupes mobiles, activez l'option Colorer les groupes mobiles. Une couleur prédéfinie est alors attribuée aux composants de chaque groupe. Cette option facilite l'analyse des relations entre composants. Pour rétablir la couleur normale des composants, désactivez l'option dans la boîte de dialogue des paramètres ou cliquez avec le bouton droit de la souris sur le noeud Groupes mobiles et choisissez Colorer les groupes mobiles.
6. Cliquez sur Toutes les positions initiales à 0,0 si vous souhaitez définir toutes les positions initiales de degrés de liberté sur 0 sans modifier la position réelle du mécanisme.

   Cette option est utile pour visionner des tracés de variable démarrant à 0 dans le graphique de sortie.

7. Cliquez sur Réinitialiser tout pour rétablir la position initiale de tous les systèmes de coordonnées, position établie lors de la construction du système de coordonnées de liaison .

   Il s'agit de la configuration par défaut.

8. Cliquez sur Analyse des contraintes AIP pour préparer toutes les informations MEF nécessaires à l'analyse des contraintes AIP.

   Cette fonction enregistre les données MEF dans les fichiers pièce correspondant aux pièces sélectionnées.

9. Une autre solution consiste à cliquez sur Simulation ANSYS pour préparer un fichier contenant toutes les informations MEF nécessaires à l'exportation vers ANSYS.

   Cette fonction permet d'enregistrer les données MEF pertinentes dans un fichier pouvant être lu par ANSYS.

   • Dans la zone de texte, entrez le nom du fichier contenant toutes les informations MEF pour l'exportation vers ANSYS.
   • Vous pouvez également cliquer sur Enregistrer dans pour spécifier un fichier existant ou créer un fichier.

     Si vous sélectionnez un fichier existant, le logiciel remplace toutes les données qu'il contient.

     Remarque : Si vous utilisez Ansys Workbench version 10 ou 11, effectuez une modification supplémentaire dans le fichier. Ouvrez le fichier texte et repérez la section intitulée "Inertial State". Deux lignes de cette section doivent être supprimées. Il s'agit de la ligne "Grounded" et du code correspondant (0 ou 1) indiqué à la ligne suivante.
10. Cliquez sur Autres pour afficher davantage de propriétés.
11. Pour afficher vos informations de copyright sur les fichiers AVI générés, cliquez sur Afficher un avis de copyright sur les AVI et entrez vos informations de copyright dans la zone de texte.
12. Cliquez sur Entrer la vitesse angulaire en tours par minute (tr/min) pour saisir des vitesses angulaires en tours par minute.

    Cependant, le résultat est exprimé selon les unités définies lorsque vous avez sélectionné le fichier d'ensemble vide.

13. Pour définir la longueur de l'axe Z du système de coordonnées de l'ensemble pour les repères 3D dans la fenêtre graphique, entrez la valeur de pourcentage dans la zone d'édition de la taille de l'axe Z.

    Par défaut, la taille de l'axe Z est égale à 20 % de la diagonale de la zone de délimitation.

14. Cliquez sur OK ou Appliquer.

    A la différence du bouton Appliquer, le bouton OK ferme la boîte de dialogue après avoir enregistré vos paramètres.

Modèle de mécanisme micro

Cette option est destinée aux mécanismes dont les propriétés massiques sont peu élevées.

Le mode standard, le calcul échoue si la masse ou l'inertie est inférieure à 1e-10 kg ou 1e-16 kg.m2. Une procédure Gauss permet alors de résoudre l'équation dynamique, avec une précision de 1e-10 (en dessous de cette valeur, le pivot est fixé à 0).

Si l'option Modèle de mécanisme micro est activée, la masse ou l'inertie doit être supérieure à 1e-20 kg ou 1e-32 kg.m2. La précision de Gauss est fixée à 1e-32.

Pour déterminer quand activer cette option, vérifiez les propriétés massiques fournies dans le système de coordonnées de la liaison.

• En présence d'un degré de liberté de translation, nous devons vérifier la masse.
• S'il s'agit d'un degré de liberté de rotation le long de l'axe X, nous devons vérifier l'inertie principale Ixx le long de l'axe X, mais pas les inerties transversales Ixz et Ixy, car elles n'ont aucun intérêt.

Exemple 1 :
Dans le cas d'un mécanisme où la plus petite pièce a une masse m = 6.5e-9 kg et des inerties principales Ixx = 1e-20 kg/m2, Iyy = 1e-20 kg.m2, même si Izz > limite d'inertie = 1e-10 kg.m2 :
	Si cette pièce possède uniquement un degré de liberté de rotation le long de l'axe Z, le modèle de mécanisme micro n'est pas nécessaire, car Izz > limite d'inertie = 1.0e-10 kg.m2. Si cette pièce possède uniquement un degré de liberté de translation

Avertissement : Activez le modèle de mécanisme micro uniquement en cas de simulation d'un petit mécanisme. Simultanément, vous devez modifier la précision de l'ensemble pour l'optimiser pour les petites pièces. Pour en savoir davantage, reportez-vous à Précision de l'ensemble.

Précision de l'ensemble

Applicable uniquement aux cas de contact 2D et de contour fermé.

Contact 2D : définit la distance maximum autorisée entre les points de contact. La valeur par défaut est 1e-6m = 1μm.

• Cette distance est toujours vérifiée à la fin des pas Runge-Kutta.
• Si la distance entre ces points ne dépasse pas la précision de l'ensemble, les positions et les vitesses sont acceptées, et le calcul se poursuit avec l'estimation des erreurs d'intégration.
• Si la distance dépasse la précision de l'ensemble, les positions sont corrigées jusqu'à ce que la distance respecte la précision de l'ensemble. Ensuite, sur la base de ces nouvelles positions, les vitesses sont ajustées et le calcul se poursuit avec l'estimation des erreurs d'intégration.

Contour fermé : similaire au contact 2D, si ce n'est l'éventuelle présence de contraintes d'angle (exprimées en radians), en fonction du type de liaison.

• La distance et les contraintes d'angle sont vérifiées à la fin des pas Runge-Kutta.
• Si les contraintes de distance ne dépassent pas la précision de l'ensemble, et si les contraintes d'angle ne dépassent pas la précision de l'ensemble (exprimée en mètres) multipliée par 1e3, les positions et les vitesses sont acceptées, et le calcul se poursuit avec l'estimation des erreurs d'intégration.
• Sinon, les positions sont corrigées jusqu'à ce que les contraintes de distance ne dépassent pas la précision de l'ensemble et que les contraintes d'angle n'excèdent pas la précision de l'ensemble multipliée par 1e3. Les vitesses sont alors ajustées et le calcul se poursuit avec l'estimation des erreurs d'intégration.

Modification de la précision de l'ensemble

Il est possible de modifier la précision de l'ensemble dans les cas suivants :

• Il est impossible d'assembler le mécanisme au début de la simulation ou pendant. Commencez par vérifier la faisabilité du mécanisme. (La position demandée est-elle réaliste et peut-elle être atteinte par le mécanisme ? Vérifiez les mouvements imposés qui peuvent aboutir à des positions contradictoires.) En l'absence de problème évident, et si l'échelle du mécanisme est grande (de l'ordre de 1 m), augmentez la précision de l'ensemble (1e-5m ou 1e-4m). Si l'échelle est petite (inférieure à 10 mm), réduisez la précision de l'ensemble (1e-7m ou 1e-8m).
• Si la taille du mécanisme est inférieure à 1 mm, réduisez la précision de l'ensemble (1e-8m à 1e-10m) ou utilisez l'option Modèle de mécanisme micro.

Avertissement : N'imposez pas une précision de l'ensemble inférieure à 1e-12. Cela n'apporte rien et peut entraîner des problèmes de simulation.

Précision de la résolution

Les équations dynamiques sont intégrées à l'aide d'une méthode Runge-Kutta d'ordre 5. Les erreurs d'intégration et le pas temporel sont gérés de la manière suivante :

• L'erreur d'intégration est estimée à la fin de chaque pas Runge-Kutta, en fonction des vitesses et des accélérations calculées.
• Cette erreur d'intégration est comparée au paramètre utilisateur Précision de la résolution.
• Si l'erreur d'intégration n'excède pas la précision de résolution, le pas est accepté et l'intégration se poursuit.
• Si l'erreur d'intégration dépasse la précision de résolution, le pas est refusé. Un nouveau pas temporel, plus petit que le pas réel, est alors calculé. La simulation reprend à partir du début du pas avec la nouvelle valeur.

L'erreur d'intégration est estimée à l'aide de certaines propriétés des formules Runge-Kutta. Elle permet de calculer facilement les positions "p" et les vitesses "v" par rapport à l'ordre 5 (vecteurs désignés respectivement par p5 et v5) et à l'ordre 4 (vecteurs désignés par p4 et v4). L'erreur d'intégration est alors définie par rapport aux positions et aux vitesses, comme indiqué ci-dessous :

Err_intég_position = norme(p5 - p4) Err_intég_vitesse = norme(v5 - v4) Où "norme" correspond à une norme particulière.

Lorsqu'un pas est accepté, les rapports suivants existent (en unités métriques) :

Err_intég_position = norme(p5 - p4) < Atol + | p5 | . Rtol Err_intég_vitesse = norme(v5 - v4) < Atol + | v5 | . Rtol

Avec :

	Atol	Rtol
Degré de liberté de translation	Précision de la résolution Par défaut = 1e-6 Pas de valeur maximale	Précision de la résolution Par défaut = 1e-6 Pas de valeur maximale
Degré de liberté de rotation	Précision de la résolution 1e3 Par défaut = 1e-3 Valeur maximale = 1e-2	Précision de la résolution 1e3 Par défaut = 1e-3 Valeur maximale = 1e-2

Les exemples suivants illustrent ce processus :

Exemple 1 : erreur relative Rtol
Type de liaison : articulation prismatique 1 avec position et vitesse
	p[1] = 4529.289768 m v[1] = 18.45687455 m/s
Si la précision de résolution est fixée à 1e-6 (valeur par défaut), des résultats à six chiffres sont garantis :
	p[1] = 4529.28 m v[1] = 18.4568 m/s
Si la précision de résolution est fixée à 1e-8, des résultats à huit chiffres sont garantis :
	p[1] = 4529.2897 m v[1] = 18.456874 m/s
Exemple 2 : erreur relative Atol
Type de liaison : articulation prismatique 1 avec position et vitesse
	p[1] = 0.000024557 m v[1] = 0.005896476 m/s
Si la précision de résolution est fixée à 1e-6 (valeur par défaut), des résultats à six décimales sont garantis :
	p[1] = 0.000024 m v[1] = 0.005896 m/s
Si la précision de résolution est fixée à 1e-8, des résultats à huit décimales sont garantis :
	p[1] = 0.00002455 m v[1] = 0.00589647 m/s
Le même raisonnement s'applique à une articulation cylindrique, mais Atol et Rtol ont une précision de résolution identique, multipliée par 1e3 :
Exemple 3 : erreur relative Rtol
Type de liaison : articulation cylindrique 2 avec position et vitesse
	p[2] = 12.53214221 rad v[2] = 21.36589547 rad/s
Si la précision de résolution est fixée à 1e-6 (valeur par défaut), des résultats à trois chiffres sont garantis :
	p[2] = 12.5 rad v[2] = 21.3 rad/s
Si la précision de résolution est fixée à 1e-8, des résultats à cinq chiffres sont garantis :
	p[2] = 12.532 rad v[2] = 21.365 rad/s

Il est possible de modifier la précision de résolution dans les cas suivants :

• La simulation est interrompue par un message d'erreur et le pas temporel est suffisamment petit pour garantir un résultat de bonne qualité. En cas de légers décalages, réduisez la précision de résolution. En cas de gros décalages, augmentez la précision de résolution.
• Lorsque les contacts 2D sont activés (état = 1). En cas de forces légères, réduisez la précision de résolution. En cas de forces importantes, augmentez la précision de résolution. Cela ne vaut pas pour les forces aux instants de choc.
• Lorsque vous travaillez sur des petits mécanismes (inférieurs à 1 mm). Si tel est le cas, réduisez la précision de résolution ou activez l'option Modèle de mécanisme micro.

Avertissement : La précision de résolution est directement liée à la taille de pas temporel. Ne réduisez pas trop la précision de résolution (pas en dessous de 1e-12, par exemple). Sinon, le temps de simulation peut en pâtir sérieusement.

Vitesse de capture

Ce paramètre permet de simuler l'impact entre les objets. Il aide la résolution à limiter le nombre de légers rebonds avant l'obtention de résultats de contact constants. Le modèle de choc utilise un coefficient de restitution "e". La valeur, qui est spécifiée par l'utilisateur, s'échelonne de 0 à 1. Pour les conditions résultantes, les valeurs sont considérées de la manière suivante :

• Lorsque e = 0, la dissipation de l'énergie est maximale. Prenons le cas, par exemple, d'une simple balle qui tombe sur un plan, à partir d'une hauteur initiale, sans vitesse appliquée, juste sous l'effet de la gravité. Aucun rebond n'est observable, l'état du contact = 1.
• Lorsque e = 1, la dissipation de l'énergie est nulle. En suivant l'exemple de la balle, celle-ci rebondit pour revenir à sa position initiale, l'état de contact = 0.5. Le mouvement est périodique et continue indéfiniment.
• Lorsque e>0 et e<1, la dissipation d'énergie a lieu à chaque impact. Prenons l'exemple de la balle à nouveau, celle-ci rebondit, mais la hauteur du rebond diminue après chaque impact et, en ayant atteint la limite, la balle reste sur le plan, avec un état de contact au point = 1. La vitesse de capture opère dans ces cas de figure.

Le paramètre Vitesse de capture aide la résolution à limiter le nombre de petits rebond qui se produisent avant que le contact soit considéré comme actif ou constant. Le processus de capture peut se résumer comme suit :

• L'impact est calculé avec tous les coefficients de restitution fixés à leur valeur initiale.
• Les vitesses relatives après impact, qui représentent les vitesses de décollage, sont comparées au paramètre de vitesse de capture de tous les contacts.
• Si toutes les vitesses relatives sont supérieures à la vitesse de capture ou nulles, l'impact est accepté et la résolution avance dans le temps en utilisant les nouvelles vitesses comme paramètres initiaux.
• Si la vitesse relative est inférieure à la vitesse de capture, mais non nulle, e = 0 est imposé pour ce contact pour augmenter au maximum la perte d'énergie, et l'impact est recalculé. Si l'impact est accepté, tous les coefficients de restitution sont réinitialisés en fonction de leur valeur initiale.

Avertissement : L'état de contact (e = 1) n'est jamais imposé par programme. La résolution gère l'état de contact, afin que tous les contacts actifs soient cohérents. Pour le déterminer, la résolution utilise une équation quadratique non linéaire.

Quand le paramètre peut-il être modifié ?

Ce paramètre peut être modifié dans les cas suivants :

• En présence de contacts 2D, lorsque la simulation est lente. Arrêtez la simulation, tracez la vitesse de capture. Si le paramètre varie pour chaque pas temporel (entre 0 - 1 - 2) ou est égal à 1, il s'agit d'un problème de capture. La résolution tente de stabiliser l'état des contacts, mais cela n'est pas simple et prend du temps. Dans ce cas, augmentez la vitesse de capture.
• Il n'y a aucun avantage à réduire la valeur du paramètre.

Vitesse de régularisation

Pour les contacts 2D, une loi de frottement de Coulomb non linéaire est utilisée. Dans les liaisons et contacts 3D, pour une question de simplicité et pour éviter des conditions hyperstatiques, une loi de Coulomb régularisée est utilisée, qui peut être illustrée de la manière suivante :

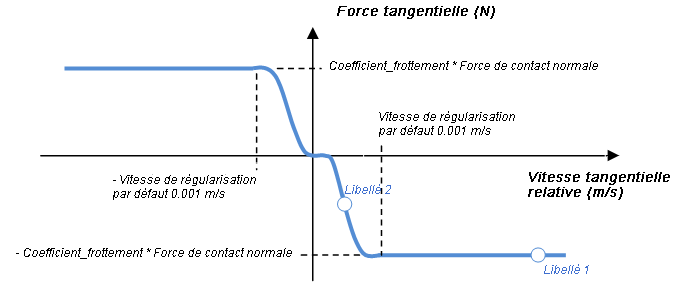
La régularisation est obtenue par le paramètre de régularisation de la vitesse.

A l'aide de ce modèle, en cas de contact collant (ou de contact roulant), lorsque la vitesse tangentielle relative est égale à zéro, la force tangentielle est nulle.

En cas de frottement de la liaison dans un degré de liberté de rotation, la force tangentielle est remplacée par un couple de torsion (unité : Nm) et la vitesse relative tangentielle est une vitesse de rotation (unité : rad/s). Les deux sont calculées en multipliant la force tangentielle et en divisant la vitesse de translation par le rayon de liaison.

Exemple 1 :
Une articulation cylindrique avec un rayon de 10 mm est pilotée avec une vitesse constante "w" égale à 10 rad/s. Nous appliquons une force (Fn) égale à 20 N à l'articulation, perpendiculaire à son axe de rotation, avec un coefficient de frottement (mu) de 0.1. Dans ce cas, le couple de torsion (Uf) qui s'applique à l'articulation peut être calculé de la manière suivante :
	? = r * w = 0.01 * 10 = 0.1 m/s ? > vitesse de régularisation = 0.001 m/s => Uf = -mu * r * Fn = -0.1 * 0.01 * 20 = -0.02 Nm Reportez-vous à "tag 1" dans le graphique de Coulomb régularisé.
Exemple 2 :
En prenant le même exemple, mais avec une vitesse (w) de 0.05 rad/s, le couple de frottement (Uf) est alors fourni par :
	? = r * w = 0.01 * 0.05 = 0.0005 m/sm ? > vitesse de régularisation = 0.001 m/s => Uf ≈ -mu * r * Fn/2 = -0.1 * 0.01 * 20/2 = -0.01 Nm Reportez-vous à "tag 2" dans le graphique de Coulomb régularisé.

Il est possible de modifier la vitesse de régularisation dans les cas suivants :

• La simulation est lente et de petites oscillations se produisent sur une liaison avec frottement ou dans une liaison de contact 3D. Le frottement dans la liaison ou le contact 3D crée une importante raideur dans le modèle, de sorte que la résolution réduit le pas temporel, afin de maintenir une précision fiable. Vous devez réduire la raideur => augmentation du paramètre de vitesse de régularisation par un facteur de 5 (5e-3 m/s). Si le modèle est toujours lent, vous pouvez continuer à augmenter le paramètre en utilisant des valeurs relatives au modèle (inférieures aux vitesses du modèle).
• N'augmentez pas trop la vitesse de régularisation, sous peine de fonctionner uniquement entre ces valeurs. La force de frottement n'atteint jamais sa valeur maximale, ce qui a pour résultat de limiter artificiellement l'effet de frottement.

Validation numérique

Avant d'analyser les résultats de simulation, il est important de vérifier que la simulation est correcte d'un point de vue numérique, à savoir qu'elle n'est pas sensible aux paramètres numériques. Pour procéder à l'étape de validation numérique, effectuez l'opération suivante :

1. Effectuez une simulation avec un ensemble de paramètres numériques (précision de l'ensemble, précision de résolution, vitesse de capture, vitesse de régularisation et pas temporel), puis enregistrez-la.
2. Divisez chaque paramètre par 10, effectuez la simulation et enregistrez-la.
3. Tracez tous les résultats sur le même graphique. Si les résultats sont similaires, la simulation n'est pas sensible aux paramètres numériques. Sinon, il existe un problème de sensibilité.
4. Les résultats peuvent être analysés en l'absence de sensibilité de la simulation.
5. Si la simulation est sensible aux paramètres numériques, utilisez les courbes de résultat pour détecter le paramètre en cause. Divisez le paramètre par 10 et utilisez la valeur obtenue comme valeur nominale du paramètre numérique. Reprenez la validation au début. Pour gagner du temps, vous pouvez vérifier l'absence de sensibilité pour le paramètre modifié.