This method uses Lanczos (Ritz) vectors and makes an excellent algorithm for solving large eigenvalue problems.
The Lanczos method involves solving the equation system of eigenvalue problems Kφ - λBφ = 0. This enables obtaining n values and eigenvectors with accuracy.
The tolerance (required convergence) of the eigenproblem solution is determined by the formula:
The tolerance parameter (tol) is defined in the Modal Analysis Parameters dialog. The accuracy of calculations can be increased by reducing the tolerance tol value. This results in the growth of the number of iterations.
Calculations
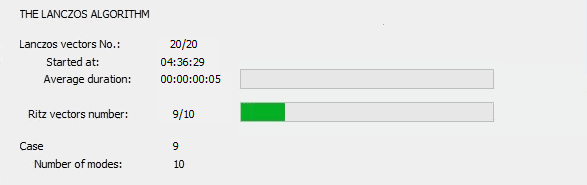
The calculations dialog for the Lanczos method shows the following phases:
- Number of the current iteration / maximum number of iterations.
- Required accuracy (tolerance).
- Accuracy of the current iteration.
- Number of required modes.
See also: