A non-linear analysis consists in the incremental application of loads. During the calculations, loads are not considered at a specific time, but they are gradually increased and solutions to successive equilibrium states are performed.
The non-linear behavior of a structure can be caused by a single structure element (structural or material non-linearity) or by a non-linear force-deformation relation in the whole structure (geometric non-linearity).
The following non-linear elements can cause a structural non-linearity:
- Compression / tension elements
- Cable elements
- Non-linear constraints (i.e. unilateral constraints or supports, releases, compatible nodes with the rigid parameter assigned)
- Material plasticity
- Non-linear hinges.
Geometric non-linearity options
The geometric non-linearity options take the actual higher-order effects into consideration and often improve the convergence of the calculation process for a structure including non-linear elements.
- P-Delta analysis
- This analysis considers the second-order effects, such as changing the stiffness of the element under the influence of the stress state in the element. It also considers the generation of moments resulting from the action of vertical forces at the nodes displaced horizontally.
- Large displacements analysis
- This analysis considers third-order effects, such as the additional lateral rigidity and stresses resulting from deformation or rotation. This effect considers additional forces arising in a deformed structure such as a beam with fixed supports on both ends, loaded by a vertical load, longitudinal forces arise and the deflection decreases.
These analysis parameters can improve the convergence of the calculation process because they consider the actual higher-order effects. This is especially useful when working with a structure which includes non-linear elements.
Two methods can be used to solve a system of non-linear equations: the Incremental method, and the Arc-length method.
Incremental method
If a structure includes non-linear elements (such as cables, unilateral supports, and material plasticity), calculations applying the incremental method are performed.
With the incremental method, the right-hand load vector is divided into n equal increments. A consecutive load increment is applied to the structure once the state of equilibrium for the previous increment is achieved. The norm of unbalanced forces is specified for each step, allowing for monitoring of the structure force-deformation relations.
The following figure shows an example of a nonlinear process using the incremental process. The values used for non-linear calculations are displayed.
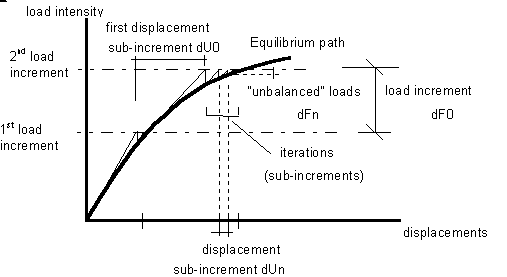
The load increment is used when dividing a load into smaller segments. For complex structures where the impact of non-linear effects is considerable, it is possible that calculations do not converge if the analysis for the value of a load is applied in one step. The number of load increments influences the number of calculation iterations. The greater the number of increments, the greater the probability for the calculations to reach the point of convergence.
Arc-length method
The arc-length method of displacement steering should be applied when the incremental algorithms of solving equations by force steering are not convergent.
The Arc-length method is applied during non-linear pushover analysis. It is strongly recommended when non-linear structure attributes are defined in a structure model (see the appendix).
Analysis process
- The Initial Stress method.
- The Modified Newton-Raphson method.
- The Full Newton-Raphson method.
In general, the Initial Stress method is the quickest one, and the Full Newton-Raphson method is the slowest. However, the probability of convergence is greater with the Full Newton-Raphson method than with the Initial Stress method.
The following table shows how to set the Matrix update options in order to use the adequate algorithm.
| Algorithm | Matrix update after each subdivision | Matrix update after each iteration |
|---|---|---|
| Initial Stress | Off | Off |
| Modified Newton-Raphson | On | Off |
| Full Newton-Raphson | On | On |
The algorithm of the Broyden-Fletcher-Goldforb-Shanno (BFGS) procedure modifies the stiffness matrix during calculations. In certain cases, using the line search algorithm can improve the convergence of the method.
When the state of equilibrium is achieved, the iteration process stops, and the convergence of the process is checked. The displacement increments dUn and the unbalanced forces dFn are essentially zero, or sufficiently small in comparison with the tolerance parameters for both values. The iteration process stops if divergence occurs. The lack of convergence can be interpreted either as the numerical effect of structure overloads, or as the result of a numerical process instability such as when the load is divided into a small number of intervals. In such cases, the number of load increments can be increased, which usually helps the process to converge.
See also: