現実の構造物は、どれも(主に摩擦により)エネルギーを放出します。このため、減衰は現実の解析で重要な成分です。一般的に、過渡的でない事象(風負荷や群集荷重など)の場合は無視され、過渡的事象(地震による荷重や爆風)の場合は重要視されます。
さまざまな種類の減衰が、動解析での減衰行列[B]を構成しています。したがって、次のようにいくつかの行列で減衰行列が構成されています。
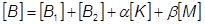

ここで、
 = 減衰要素(CVISC、CDAMPi)と B2GG DMIG からの減衰
= 減衰要素(CVISC、CDAMPi)と B2GG DMIG からの減衰
 = B2PP DMIG からの減衰
= B2PP DMIG からの減衰
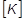 = グローバル剛性の行列
= グローバル剛性の行列
 = グローバル質量の行列
= グローバル質量の行列
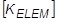 = 要素の剛性の行列
= 要素の剛性の行列
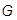 = 全体の構造減衰係数(PARAM、G)
= 全体の構造減衰係数(PARAM、G)
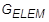 = 要素の構造減衰係数(MATi エントリの GE)
= 要素の構造減衰係数(MATi エントリの GE)
 = 全体の構造減衰を同等の粘性減衰に変換する、対象の周波数(単位時間当たりのラジアン) (PARAM、W3)
= 全体の構造減衰を同等の粘性減衰に変換する、対象の周波数(単位時間当たりのラジアン) (PARAM、W3)
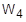 = 要素の構造減衰を同等の粘性減衰に変換する、対象の周波数(単位時間当たりのラジアン) (PARAM、W4)
= 要素の構造減衰を同等の粘性減衰に変換する、対象の周波数(単位時間当たりのラジアン) (PARAM、W4)
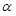 = レイリー減衰の剛性行列の尺度係数
= レイリー減衰の剛性行列の尺度係数
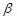 = レイリー減衰の質量行列の尺度係数
= レイリー減衰の質量行列の尺度係数
次の表に、異なる減衰項がさまざまな解析法にどう影響するかを示します。
| 周波数応答解析(直接法) | 周波数応答解析(モード法) | 過渡応答解析(直接法) | 過渡応答解析(モード法) | |
| 減衰要素 | 正常 | 結合解法に強制 | 正常 | 結合解法に強制 |
| 構造減衰 | 正常 | 正常 | 同等の粘性に変換 | 同等の粘性に変換 + 結合解法に強制 |
| モーダル減衰 | 無視 | 正常 | 無視 | 正常 |
| レイリー減衰 | 結合解法に強制 | 結合解法に強制 | 正常 | 正常 |
可能であれば、上の表で正常と記された減衰を使用するのが最も有利です。これらの組み合わせで、実行時間が最速になります。
周波数応答解析(直接法)での減衰
周波数応答解析(直接法)の問題では、複素解法を使用しています。その結果、複素減衰項をそのまま使用できます。構造減衰を同等の粘性減衰に変換する必要はありません。すべての形式の減衰をペナルティなしで使用できます。
周波数応答解析(モード法)での減衰
モーダル解析では、一般的に減衰行列が対角化しません。さらに、構造の減衰があれば、それによってやはり対角化しない複素剛性行列ができます。その結果、その種の減衰のいずれかが含まれる場合、解析が直接法として、ただしモード座標を使用して、実行される必要があります。これは、物理空間で解析するよりも速くなりますが、非連成方程式を解くほど速くはありません。非連成解析の恩恵を受けるためには、他の種類の減衰を諦めて、モーダル減衰のみ使用することが必要です。つまり、個々のモーダル自由度を個別に減衰します。
過渡応答解析(直接法)での減衰
過渡応答解析では複素係数の使用が認められません。したがって、構造減衰が同等の粘性減衰の方法で含まれています。
粘性減衰力は、減衰係数 b と速度の関数のです。これは、[B]行列と速度ベクトルを使用した運動方程式で表される誘起力です。

ここで、
 = グローバル質量の行列
= グローバル質量の行列
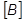 = グローバル減衰の行列
= グローバル減衰の行列
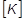 = グローバル剛性の行列
= グローバル剛性の行列
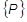 = グローバル荷重のベクトル
= グローバル荷重のベクトル
 = グローバル加速度のベクトル
= グローバル加速度のベクトル
 = グローバル速度のベクトル
= グローバル速度のベクトル
 = グローバル変位のベクトル
= グローバル変位のベクトル
この構造減衰力は、変位依存の減衰です。構造減衰力は、構造剛性行列の複素成分と減衰係数 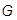 の関数です。
の関数です。
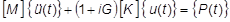
単一の自由度系に対して振幅が一定の振動応答があると仮定すると、2 つの減衰力は次の条件において同一となります。
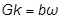
または
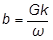
したがって、構造減衰 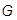 を同等の粘性減衰 b を使用してモデル化するのであれば、その同一性は 1 つの周波数でのみ保たれます(下図を参照)。
を同等の粘性減衰 b を使用してモデル化するのであれば、その同一性は 1 つの周波数でのみ保たれます(下図を参照)。

2 つのパラメータが、構造減衰を同等の粘性減衰に変換するために使用されます。全体的な構造減衰係数を、PARAM, W3, r を使用して系全体の剛性行列に適用することができます。ここで、r は、減衰が同等になる円振動数です。このパラメータは、PARAM, G と共に使用されます。W3 の既定値はゼロです。これにより、この発生源からの減衰が過渡解析で無視されます。
PARAM, W4 は、要素の構造減衰を同等の粘性減衰に変換するために使用される、代替パラメータです。PARAM, W4, r が使用されます。ここで、r は減衰が同等にされる円振動数です。PARAM, W4 は、MATi エントリに対して GE フィールドと共に使用されます。W4 の既定はゼロです。これにより、この発生源からの減衰が過渡解析で無視されます。
PARAM, W3 と PARAM, W4 の単位は、単位時間当たりのラジアンです。W3 または W4 の選択は、減衰が活発になる支配的周波数にするのが一般的です。多くの場合、最初の固有振動数が選択されますが、孤立した個別要素の減衰がさまざまな周波数で発生する可能性があり、それらは適切なデータを入力することで処理することが可能です。
過渡応答解析(モード法)での減衰
過渡応答解析(モード法)では、構造体のモード シェイプを使用してサイズを縮小し、運動方程式の連結を解き、数値的統合の効率を高めます。
手順の概要を示すために、運動している有限要素系の一般平衡方程式をまず検証します。

物理座標  からモード座標
からモード座標  への変換は次のとおりです。
への変換は次のとおりです。

モード シェイプ  は、グリッド ポイントの振る舞いではなくモードの振る舞いについて問題を変形させるために使用されます。
は、グリッド ポイントの振る舞いではなくモードの振る舞いについて問題を変形させるために使用されます。
モーダル減衰が使用されると仮定すると、この一般平衡方程式は次のように書き換えることができます。
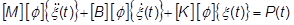
これで、モード座標から見た運動方程式になりました。方程式の連結を解くために、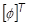 を左から掛けると、次の式が得られます。
を左から掛けると、次の式が得られます。
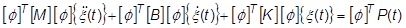
ここで、
 = 質量のモード行列または一般化行列
= 質量のモード行列または一般化行列
 = 剛性のモード行列または一般化行列
= 剛性のモード行列または一般化行列
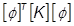 = 減衰のモード行列
= 減衰のモード行列
 = モーダル力ベクトル
= モーダル力ベクトル
モード シェイプが直交する特性を使用すると、対角線の一般された質量、剛性、および減衰(モーダル減衰)について、運動方程式を公式化することができます。これらの行列は運動方程式を連結する非対角項を持っていないため、モード運動方程式の連結が解かれます。運動方程式は次のように記述することができます。

ここで、
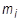 = i 番目のモーダル質量
= i 番目のモーダル質量
 = i 番目のモーダル減衰
= i 番目のモーダル減衰
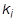 = i 番目のモーダル剛性
= i 番目のモーダル剛性
 = i 番目のモーダル力
= i 番目のモーダル力
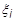 = i 番目の自由度
= i 番目の自由度
上の式は次のように書き換えることができます。
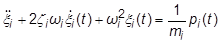
ここで、
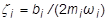 = モーダル減衰比
= モーダル減衰比
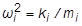 = モード周波数
= モード周波数
そして、次の式を使って個別のモード応答の総計から物理応答が回収されます。

|
前のトピック: 過渡応答解析 |