過渡応答解析は、強制した動的応答を計算する際の最も一般的な方法です。過渡応答解析の目的は、時間とともに変化する励振を受ける構造物の特性を判定することです。非定常の励振は、時間領域で明示的に定義されます。構造物に適用される負荷は、時間の各瞬間で分かっています。荷重は、加えられる力や強制動作などの形式になります。過渡応答解析から得られた結果は、一般的に、グリッド ポイントの変位、速度、加速度、および出力時間ステップごとの要素内の力と応力です。
構造物と荷重の性質に応じて、次の 2 種類の異なる数値法が過渡応答解析に使用できます。
- 過渡応答解析(直接法): 時間に対する荷重へのシステムの応答を計算します。システムに掛かる荷重は、時間とともに変化する場合もあれば、時間とともに発達する可能性のある単なる初期条件の場合もあります。この方法は、高周波数の励振に多数のモードの抽出が必要なモデルの場合に、より効率的です。また、構造減衰を使用する場合、直接法を使用する必要があります。
- 過渡応答解析(モード法): これは、動力学で使用できる代替技術です。構造物のモード形状を利用し、解析の自由度を下げ、実行時間が大きく変わります。このアプローチでは、物理自由度を、数を減らしたモーダル自由度に置き換えます。自由度の数が少ないため、解析時間が短縮されます。これは、時間ステップ数の多い非定常モデルの場合に時間が大幅に節約できます。過渡応答解析(モード法)では構造物のモード形状が使用されるため、この解析は固有値解析から自然に発展したものです。
過渡応答解析(直接法)の理論
過渡応答解析(直接法)では、直接数値積分法を使用した一連の結合方程式を解くことで構造の応答が計算されます。使用される方法は、非線形過渡応答の方法と同じで、アダプティブ時間ステップ アルゴリズムを可能にします。まず、行列形式の動的運動方程式から始めます。
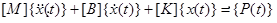
基本的な構造応答(変位)は、個別の時点(一般的には一定間隔の連続した時点)で計算されます。この解析手法は中央有限差分法と呼ばれ、後続の時点での変位、速度、加速度を調べ、それらの現在と過去の値を求めます。下の図は、過渡積分のグラフです。
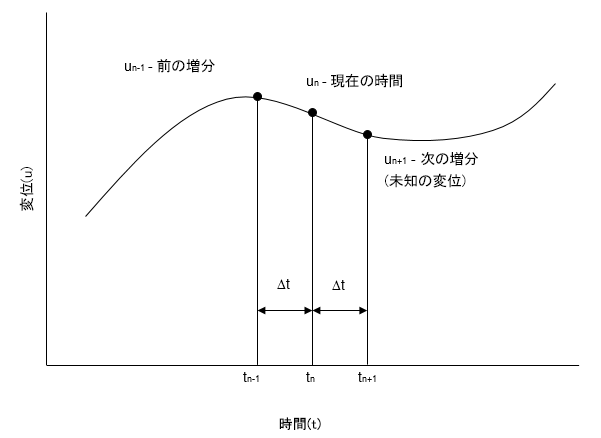
任意の時点 n で、変位、速度、加速度が分かります。この情報を使用すれば、後続のステップで変位、速度、加速度を調べる方法が多くあります。たとえば、現在の速度が次の増分まで一定のままだと仮定すると、次の変位 
は単純に現在の場所 + 速度 x 時間増分 
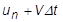になります。しかし、速度一定でない場合、つまり速度一定を前提にできない一般的な問題では、速度の変化を計算に入れなければならず、そのため方程式に加速度の項が入っています。
これは、現在の加速度が次の増分まで一定であると仮定するなら、真です。しかし、一般的な問題では、必ずしもこのようには想定できません。平均値の定理で加速度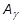 
は、「加速度が n と n+1 における加速度の加重平均になるような定数ガンマの関数である」と仮定します。
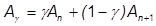
Newmark は 0.5 がガンマに適した値であると次のように示しました。
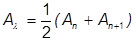
および
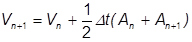
変位の最初の導関数が速度で、2 番目が加速度であるため、それらは通常は導関数としてドット表記で表現されます。
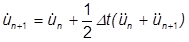
ただし、加速度は時間とともに変化する可能性があるため、変位が速度と加速度の両項によって修正されることを提案できます。ゆえに、
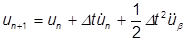
上の項の加速度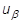 
は、上の速度と同様に次のように計算されます。
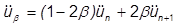
u はベータ定数として書くことができます。
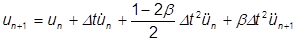
上式のベータの値は、Newmark-Beta と呼ばれ、0 と 1 の間で変化します。これは通常 ¼ で使用されます。これは平均等加速度法です。ここで、
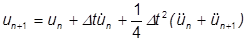
これらの方程式は、操作することによって現時点の増分における速度と加速度の式にすることができますが、過去と後続との時間間隔における変位で表します。
これらの表現は運動方程式に代入され、次の結果となります。
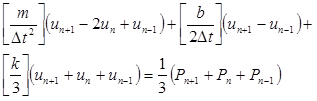
しかし、 が不明なため、解析の各式に の値が必要です。ここでは、現時点の変位を、隣接する時間での平均値で示します。同様に、荷重は 3 つのステップでの平均を取ることができ、違いは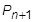 
が入力値であるということが分かっている点です。
これらの平均値を使用して次の式が成り立ちます。
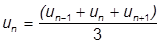
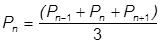
項を移動させて、左辺に未知の 、右辺に 
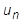と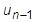 
を配置しました。
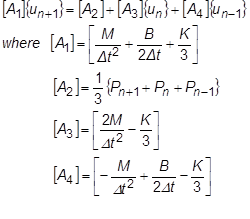
この方程式を解くには、4 つの A 項を計算し、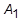
項を分解(反転)して を求めます。ここで注目したいのは、固定時間ステップを使用する問題では 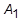を 1 回のみ分解すればよいということです。しかし、時間ステップが変わるのであれば、再度計算する必要があります。このことから、時間ステップは、変更によるコストを上回るメリットが生まれる場合を除き、固定するほうが望ましいと言えます。
過渡応答解析(モード法)の理論
過渡応答解析(モード法)を実行するには、物理座標をモード座標に変換する必要があります。これには、直交性の特性を持つ固有振動数や固有ベクトルが適しています。そこで、物理座標 u は、次のようにモード座標に置き換えることができます。
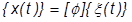
基本的な運動方程式は、次のようになります(ここでは減衰項を無視)。
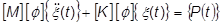
これを次のように、使いやすい式に変形します。
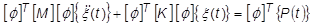
ただし、質量と剛性の項は、一般化したモード行列、すなわち扱いやすい対角行列になりました。
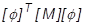= 質量のモード行列または一般化行列
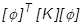= 剛性のモード行列または一般化行列
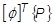= モーダル荷重ベクトル
対角行列には、モーダル自由度の連結を解く効果があります。荷重の項はベクトルで、すでに連結が解かれています。その結果、この系は一連の結合方程式として簡単に解くことができます。
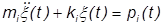
ここで、m および k は、それぞれのモーダル自由度における一般化された質量および剛性の値であり、p はモーダル荷重ベクトルです。
モーダル変位 
について値が求められたら、モーダル変位の合計から物理変位が求められます。
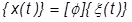
このアプローチは、モーダル自由度(DOF)がすべて座標変換に含まれている場合、直接法と正確に同じ解が得られます。ただし、このアプローチの強さが現れるのは、物理自由度よりモーダル自由度が明らかに少なくても、正確な値に近い解が普通に得られるためです。DOF が少ないことで、解析が遥かに高速になります。これは、大きなモデルや多くの時間ステップを必要とするモデルで、特に効率が高くなります。
|
前のトピック: 周波数応答解析の演習 |
次のトピック: 動解析の減衰 |