モーダル解析または固有振動数解析(固有値解析とも呼ばれる)は、他のいくつかの動解析の基本を形成し、モーダル アプローチの定式化と応答スペクトル解析も実行します。さらに、モーダル解析の結果は、動的な系があるのかどうかも含めてモデルの動的特性に関する疑問を解明してくれます。このため、解析する人は固有値解析をまず実行してからモデルの基本的な動特性を検証し、モデル化の問題をチェックする場合が多いのです。
この解析の結果からモード シェイプと周波数が分かります。ここで、出力のモード シェイプは最大値が 1.0 に設定された固有ベクトルであることに注目してください。したがって、結果の変形量は、構造体内の最大の変形が 1.0 になるように計量され、実際の振動時に予期される変形の規模は表していません。
固有値解析では、拘束を含めても含めなくても構いません。拘束なしで実行されたモデルは「自由」モードなので、最初の 6 つの振動周波数が基本的に 0 になります。部分的に拘束されたモデルには、6 未満の「自由」モードがあります。
固有値理論
動的システムを考えます。一般的に、運動方程式は系の質量、剛性、減衰、適用荷重の関数で表すことができます。
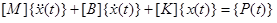
ここで、
[M] = グローバル質量の行列
[K] = グローバル剛性の行列
[B] = グローバル減衰の行列
{P} = グローバル荷重のベクトル
減衰や適用荷重がない場合、固有値または固有振動数が求められます。そして、自由振動の運動方程式を次のように記述することができます。
正弦波の振動であると仮定します。このとき、変位は次のように記述できます。
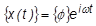
そして、{x(t)} 項を上記に置き換え、正弦波振動の場合、次に示すように加速度は変位の二次導関数だと考えます。
したがって、運動方程式が次のようになります。
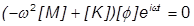
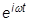はゼロにならないため、この方程式を一般的な固有値問題の形式に変形することができます。Inventor Nastran が固有値の問題を解いて固有振動数を決定します。
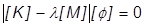
ここで、
[K] = グローバル線形剛性の行列
[M] = グローバル質量の行列
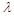= 固有振動数が生じる各モードの固有値 = 
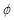= 固有モード シェイプを示す各モードの固有ベクトル
固有値とシステムの固有振動数には、次の関係が成り立ちます。
ここで、
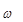= 円振動数(ラジアン/秒)
またはヘルツ単位で:
ここで、
f = 巡回周波数(ヘルツ)
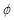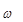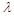解の 1 つは自明( = 0)ですが、 の他の解は考えるに値します。 は固有値 と呼ばれ、それぞれに固有ベクトルと呼ばれる一意の 
が付随しています。
上記の固有値問題を解くにあたって、拘束のない自由度の数と同じくらい多く、固有値および対応する固有ベクトルが存在します。ただし、実用的な意味を持つのは、たいてい最も低い固有周波数のみです。この周波数は常に、抽出される最初のモードになります。
固有値問題の解を得るのは困難で、多数のさまざまなアプローチが数年にわたって開発されてきました。現在、高速かつ正確で堅牢なランチョス法のアプローチが有利です。Inventor Nastran では、サブスペース法も使用できます。これは、ランチョス法が失敗する珍しいケースでのみ使用できます。SUBSPACE の選択には、[パラメータ]ダイアログ ボックスの[プログラム コントロール設定]で Nastran 命令の EXTRACTMETHOD=SUBSPACE が使用されています([高度な設定]チェックボックスをまずオンにする)。詳細は、『ユーザ ガイド』の「パラメータ」トピックを参照してください。このパラメータで既定の[自動]の設定は、ほとんどの情況でランチョス法を使用しますが、一部の小さな問題ではサブスペースに変わります。Inventor Nastran は、他の Nastran で他の抽出方法の使用に利用可能な EIGR カードを認識しません。
また、求められた 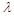が正確な固有値である一方、固有ベクトルは適当に縮尺されています。つまり、これらのベクトルは固有の大きさを持ちません。単に形状を表しています。Inventor Nastran の既定では、ベクトルに対し質量スケールを実行します。これは、方程式からモデルの一般化質量を計算することによって行われます。
ベクトルの項のすべてをそれで割ります。そのことで、ベクトルが見た目には任意に縮尺変更されますが、それは数学的に重要な特性を持ち、他の用途で利用できる可能性があります。質量の縮尺変更に加え、Nastran では最大縮尺変更も使用できます。これはベクトルの最大値を 1.0 にします。この方法では、小さなベクトルを手作業で検査することができます。
固有ベクトルの特性は、それらが直交するということです。これは、固有ベクトルを他の固有ベクトルで割ると単位行列ができることを意味します。固有ベクトルをそれ自身で乗算すると、ゼロになります。
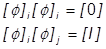
これは、ダイナミクス解析で利用されるもう一つの特性です。
剛体モード
固有値解析は、拘束に基づいて通常は次のように 2 つのタイプに分けられます。
- モデルが拘束されていない場合(ロケットや飛行中の飛行機など)、対応するビームの表現、すなわちこの方法で解析されたビームが両端で自由になることから、これを自由-自由解析と呼びます。自由-自由系でモーダル解析を実行すると、弾性モードに加えて 6 つのゼロ周波数剛体モード (またはメカニズム モード)が求められます。これらのモードは、自由な移動と回転を 6 つの運動方向に表現して、それらをモード 1 からモード 6 に抽出します。モード 7 は最初のフレキシブル モードと呼ばれ、ゼロ エネルギー モードにはなりません。このようなモードを検知できることを確認するためには、モデルの検査には拘束なしでの固有値解析の実行が常に好ましいと言えます。このようにすれば、モデルが偶発的に内部で拘束されてはいないことが分かります。一部の系では実際に拘束されておらず、静的解析とは異なり、自由-自由構造で固有値解析を正常に実行することができます。
- 他のタイプの固有値解析は、拘束された系です。この場合、ゼロ周波数モードがないことが求められます。検出された場合は、それはモデルの一部が剛体のように自由に動くこと意味します。通常、このタイプの運動をメカニズムと呼びます。そしてこのタイプの問題を固有値解析で解くことができる一方、静解析は失敗します。このため、固有値解析は、静解析が失敗したときのデバッグ ツールとしてよく使用されます。ゼロ周波数モードのソースが識別されたら、それが拘束でき、静解析が正常に実行されます。
メカニズム モードは、構造の一部が剛体として移動するような不十分に拘束された構造で発生します。ヒンジやボール ジョイントに接する平たい板がその一例です。メカニズム モードは、構造内のパーツ同士がしっかり接続されていない場合にも発生します。ソリッド要素に接続されたバーがこの典型例です。
剛体やメカニズム モードは、ゼロ周波数またはゼロに近い周波数の固有値で示されています。ほとんどの構造物において、1.0E-3 Hz 付近かそれ以下でゼロに近くなり、負の値になる場合もあります。