Metoda interpolacji punktów sąsiednich umożliwia oszacowanie rzędnej (współrzędnej Z) dowolnego punktu (p) na podstawie zbioru punktów o znanych rzędnych.
Podczas obliczania średniej ważonej rzędnych naturalnych sąsiadów punktu p metoda NNI korzysta z informacji uzyskanych z triangulacji znanych punktów. Liczba sąsiadów (liczba punktów, których wartości Z są uśredniane w celu uzyskania wartości interpolowanej) zależy od triangulacji: jest liczbą punktów, z którymi nowy punkt (p) zostałby połączony, jeśli byłby wstawiony do danej powierzchni:
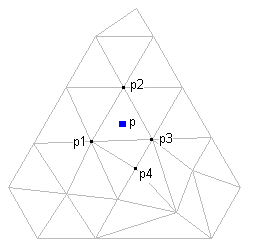
W metodzie interpolacji metodą punktów sąsiednich należy określić tylko wyjściowe położenia interpolowanych punktów. Rzędne generowanych punktów są zawsze równe średniej ważonej rzędnych istniejących punktów sąsiadujących. Rezultaty użycia metody NNI są bardziej przewidywalne niż w przypadku metody optymalnej predykcji. W metodzie NNI interpolacja jest wykonywana tylko w obrębie powierzchni, podczas gdy w metodzie optymalnej predykcji może ona wychodzić poza granice powierzchni, jeśli zostanie zaznaczony akurat taki wielobok.