Przyjęte oznaczenia:
E — moduł Younga,
G — moduł Kirchhoffa,
ν — współczynnik Poissona,
fd — ograniczenie sprężystości,
Ax — powierzchnia przekroju poprzecznego,
Ix — moment bezwładności przy skręcaniu,
Iy — moment bezwładności przy zginaniu w płaszczyźnie XZ,
Iz — moment bezwładności przy zginaniu w płaszczyźnie YZ,
ky, kz — współczynniki poprawkowe dla sztywności ścinania w kierunku Y i Z,
L — długość pręta.
-
Wstępne uwagi i założenia
Przyjęte zostały następujące założenia dla elementów prętowych (belkowych):
- Jednolite sformułowanie dla 2D i 3D (ramy 2D i 3D, ruszty).
- Jednolity element umożliwiający analizę materiałowo lub geometrycznie nieliniową.
- Standardowe stopnie swobody przemieszczenia w 2 węzłach skrajnych.
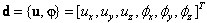
- Dopuszczalne jest wykorzystanie:
- wpływu ścinania (model Timoshenki),
- zmiennego przekroju — tylko dla nieliniowości geometrycznej,
- podłoża Winklera.
- Dostępne są dwa poziomy nieliniowości geometrycznej: P-Delta (teoria II rzędu) i Duże przemieszczenia, która jest możliwie najdokładniejszą teorią dla dużych przemieszczeń i obrotów; jest to podejście przyrostowe z aktualizacją geometrii.
- W granicy przy założeniu małych przemieszczeń i braku nieliniowości fizycznych wyniki są identyczne jak w standardowych elementach liniowych.
- W analizie nieliniowości materiałowej stosuje się podejście warstwowe i konstytutywne prawo naprężenia—odkształcenia dla stanu jednoosiowego na szczeblu punktu (warstwy).
- Stany ścinania i skręcania są traktowane jako liniowo sprężyste i nie sprzężone ze stanem sił osiowych/zginania na szczeblu przekroju.
- Zwolnienia i przeguby o charakterystyce nieliniowej mogą być zdefiniowane jedynie jako elementy DSC.
- Dopuszczalne są wszystkie rodzaje obciążeń elementowych (tak jak dla standardowych elementów). Jednakże zakłada się, że siły węzłowe działające na konstrukcję są wyznaczane na początku procesu. Nie są uwzględniane zmiany w przekazywaniu się obciążeń elementowych do węzłów wywołane nieliniowością geometryczną bądź materiałową.
- Oprócz elementu sprężysto—plastycznego możliwa jest również generacja przegubów sprężysto—plastycznych w wybranych przekrojach pręta jako rozszerzenie opcji „przeguby nieliniowe” (patrz punkt 5).
-
Geometria, kinematyka i aproksymacja pola deformacji
Geometria, konwencja znakowania sił, przemieszczeń, naprężeń i odkształceń
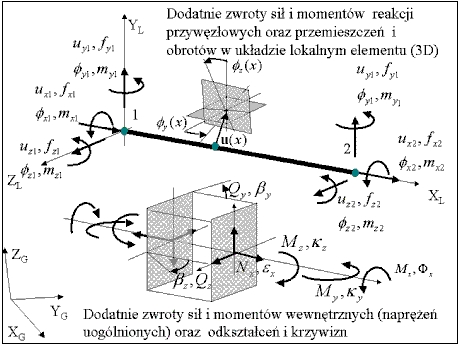
Podstawowe zależności kinematyczne
W układzie lokalnym elementu w zakresie geometrycznie liniowym odkształcenia uogólnione E na poziomie przekroju wynoszą (symbol (
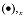oznacza różniczkowanie wzdłuż kierunku osi pręta):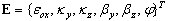 
gdzie:
Odkształcenie podłużne w osi pęta:
e0x = u ,x
Krzywizny:
K y = fy'x
K z = — f z'x
Średnie kąty (odkształcenie):
b y = n 'x — f z'
b y = w 'x — f y
Jednostkowy kąt skręcenia:
j = f x'x
Aproksymacja pola przemieszczeń
Z uwagi na możliwość uwzględnienia wpływu ścinania i zgodności wyników uzyskanych dla elementu liniowego wprowadzone zostały tak zwane fizyczne funkcje kształtu uwzględniające wpływ ścinania.
Pręty 2D:
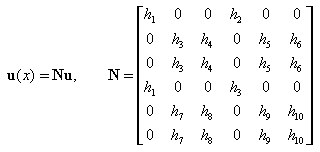
Funkcje kształtu i ich pochodne są wyrażone wzorami:
gdzie:
x = x / L
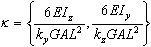odpowiednio dla płaszczyzn XY i XZ. Zależności kinematyczne w zapisie macierzowym (teoria geometrycznie liniowa)
Przy uwzględnieniu wpływu odkształceń narzuconych
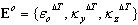
Przyrost odkształceń uogólnionych (przekrojowych):
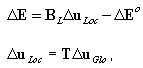
2D:
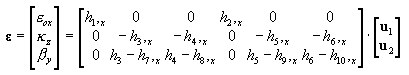
3D:
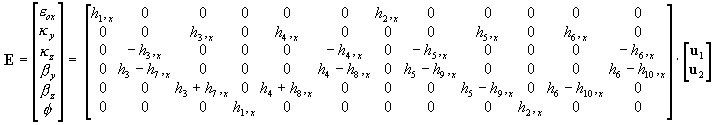
gdzie:
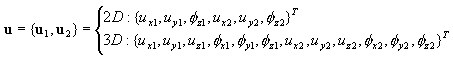
Odkształcenia w punkcie (warstwie)
Mając dane odkształcenia uogólnione {ε 0x, k y , k x } przekroju, odkształcenie e xl lub jego przyrost De xl w dowolnym punkcie przekroju l o współrzędnych yl, zl, wyznaczany jest jako:
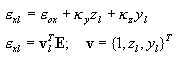
ostatecznie przyrost odkształcenia w warstwie:
-
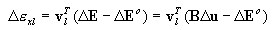
Naprężenia i siły wewnętrzne w elemencie
Prawo konstytutywne na szczeblu punktu
Przyjmuje się je w postaci ogólnej, przyrostowej, gdzie naprężenia aktualne σx n + 1 wyznacza się jako funkcję naprężenia w ostatnim stanie równowagi σx n i aktualnego przyrostu odkształceń z uwzględnieniem odkształceń narzuconych (termicznych),
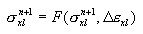
bazując na funkcji σ = f(ε) opisującej zależność w procesie aktywnego obciążenia i na specyfikacji prawa odciążenia i powtórnego obciążenia. W szczególności może to być prawo sprężysto—plastyczne ze wzmocnieniem liniowym i wyspecyfikowanym prawem odciążenia, tj. (a) sprężyste, (b) plastyczne, (c) zniszczenie, (d) mieszane. Dla odciążenia sprężystego proces bierny i aktywny odbywa się po tej samej ścieżce σ = f (ε). Dla pozostałych odbywa się po prostej określonej początkowym punktem danego procesu odciążenia {ε UNL, σ UNL }i modułem odciążenia D UNL wyznaczanym jako
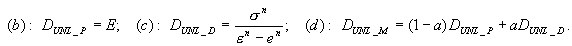
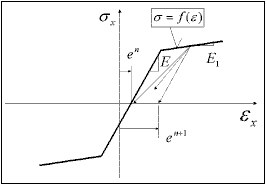
e n jest zapamiętanym odkształceniem, przy kórym rozpoczął się aktualny proces czynny, rozpoczęty po przejściu przez 0 w naprężeniach przy odciążaniu (e 1 = 0).
W analizie konieczna jest też aktualna sztywność rozumiana jako pochodna
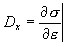
Wyznaczanie sił i sztywności przekrojowych.
Na poziomie przekroju wektor sił wewnętrznych (naprężeń uogólnionych) tworzą:
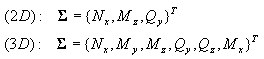
Stany ścinania i skręcania ΣST są traktowane jako liniowo sprężyste i nie sprzężone ze stanem sił osiowych/zginania na szczeblu przekroju.
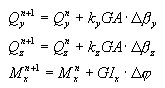
Stany ściskania/rozciągania Σ NM są ogólnie traktowane jako sprzężone, gdy stosowane jest podejście warstwowe, jednak dopóki zagwarantowany jest stan sprężysty, tj. dopóki aktualne odkształcenia uogólnione spełniają następujący warunek stanu sprężystego:
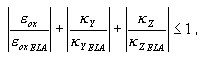
gdzie:
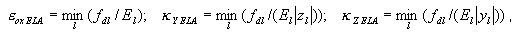
przekrój traktowany jest jako sprężysty i podejście warstwowe nie jest uaktywniane.
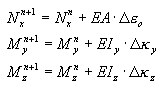
Po stwierdzonym naruszeniu warunku stanu sprężystego naprężenia wywołane odkształcenami osiowymi i zginaniem są wyznaczane osobno dla każdej warstwy i na ich podstawie wyznaczane są wielkości przekrojowe.
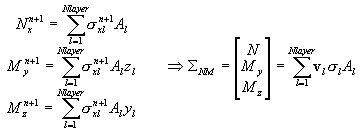
Sztywność na poziomie przekroju D jest wyznaczana w następujący sposób:
w stanie sprężystym jako:
D = diag {EA, EIy, EIz, KyGA, kzGA, GIx)
Po przekroczeniu warunku stanu sprężystego jako:
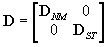
gdzie:
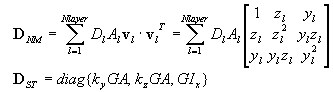
Wektor sił węzłowych i macierz sztywności elementu
Wyznaczane są wzorami standardowymi, przy użyciu kwadratury Gaussa (Ngauss=3).
-
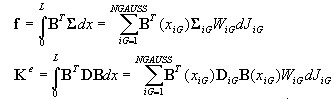
Nieliniowość geometryczna
Rozważa się następujące konfiguracje:
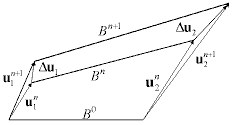
B0 — konfiguracja początkowa
Bn — konfiguracja odniesienia (ostatnia, dla której spełnione są warunki równowagi)
Bn + 1 — konfiguracja aktualna (iterowana)
Punktem wyjścia sformułowania elementu jest zasada prac wirtualnych, zapisana dla przyrostów przemieszczeń w formie:
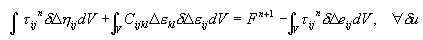
gdzie: Δε — przyrost odkształcenia przy przejściu Bn do Bn+1, Δe, Δη są jego częściami, odpowiednio: liniową i nieliniową względem przyrostu przemieszczeń Δu, natomiast τ jest naprężeniem odniesionym do konfiguracji odniesienia, a Cijkl jest tensorem stycznych modułów sprężystości.
Opcja Nieliniowość
Odpowiada sformułowaniu nieliniowemu, tj. teorii II rzędu. Ze względu na możliwą nieliniowość materiałową wprowadza się sformułowanie przyrostowe (jednak bez modyfikacji geometrii elementu).
Zależności kinematyczne
Przyrosty odkształceń w zapisie macierzowym:
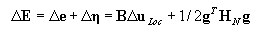
gdzie:
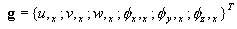
gradient przyrostu przemieszczeń g = ΓΔu
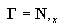
natomiast
jest macierzą wyboru.
Wektor sił węzłowych i macierz sztywności elementu
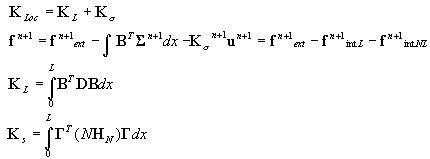
Algorytm na poziomie elementu
Nie następuje modyfikacja geometrii elementu, transformacja local—global jest przeprowadzana przy użyciu początkowej macierzy transformacji 0 T
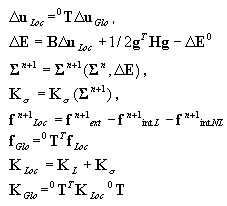
Duże przemieszczenia
Jest to pewien wariant opisu pręta z dopuszczeniem dużych przemieszczeń. Wykorzystuje się podejście uaktualnianego opisu Lagrange'a.
Wektor sił węzłowych i macierz sztywności elementu
-
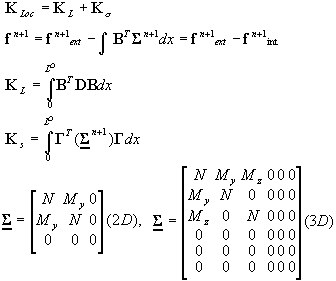
Przeguby sprężysto—plastyczne
Alternatywnie, sprężysto—plastyczną pracę konstrukcji można modelować, wprowadzając przebuby nieliniowe w wybranych przekrojach pręta. Charakterystyka przegubu, reprezentowanego przez 2-węzłowy element typu DSC, tworzy się, wykorzystując algorytm analizy przekroju opisany w punkcie 3, przy czym rolę odkształceń uogólnionych E pełnią wzajemne przemieszczenia węzłów (odniesione do kierunków lokalnych pręta) podzielone przez przyjętą (fikcyjną) długość elementu (ΔL) równą minimalnej wysokości przekroju. Pełnią one rolę objętości elementu dV=ΔL. Siły i przemieszczenia nowo utworzonych węzłów elementu DSC stanowią globalne stopnie swobody, to znaczy nie są one kondensowane.
Algorytm na szczeblu elementu-
wyznaczenie odkształceń uogólnionych w przekroju
-
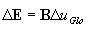
wyznaczenie sił wewnętrznych (naprężeń uogólnionych) i sztywności przekroju zgodnie z punktem 3.2
-
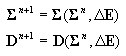
wyznaczenie sił (reakcji na końcach pręta) i sztywności elementu DSC
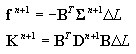
gdzie:
-
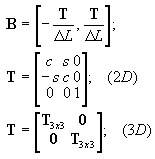