Analiza nieliniowa polega na przyrostowym przykładaniu obciążeń. W obliczeniach obciążenia nie są uwzględniane w danym momencie, ale są stopniowo zwiększane i rozwiązywane są kolejne stany równowagi.
Nieliniowe zachowanie się konstrukcji może być związane z pojedynczym jej elementem (nieliniowość konstrukcyjna bądź materiałowa) lub może wynikać z nieliniowego związku pomiędzy siłami a deformacją w całej konstrukcji (nieliniowość geometryczna).
W przypadku następujących elementów nieliniowych może wystąpić nieliniowość konstrukcyjna:
- Elementy pracujące tylko na ściskanie albo rozciąganie
- Elementy kablowe
- Nieliniowe więzy (np. więzy jednostronne lub zdefiniowane funkcją sztywności: podpory, zwolnienia, węzły kompatybilne)
- Plastyczność materiałowa
- Przeguby nieliniowe.
Opcje nieliniowości geometrycznej
Poprzez włączenie opcji nieliniowości geometrycznej możliwe jest uwzględnienie rzeczywistych efektów wyższego rzędu, co często skutkuje polepszeniem zbieżności procesu obliczeń konstrukcji zawierającej elementy nieliniowe.
- Analiza P-delta
- W tej analizie uwzględnione są efekty drugiego rzędu, tzn. zmieniająca się sztywność elementu pod wpływem stanu naprężenia w elemencie. Pod uwagę wzięta jest także generacja momentów wynikających z działania sił pionowych w węzłach przesuniętych poziomo.
- Analiza dużych przemieszczeń
- W tej analizie uwzględnione są efekty trzeciego rzędu, tzn. dodatkowa sztywność poprzeczna i naprężenia powstałe przy odkształceniu lub obrocie. Efekt ten uwzględnia powstanie dodatkowych sił w odkształconej konstrukcji (przykładowo w obustronnie zamocowanej belce obciążonej pionowo pojawiają się siły podłużne i zmniejsza się ugięcie).
Rezultatem tych parametrów może być poprawa zbieżności procesu obliczeń, ponieważ dzięki nim możliwe jest uwzględnienie rzeczywistych efektów wyższego rzędu. Jest to szczególnie przydatne przy pracy z konstrukcją, która zawiera elementy nieliniowe.
Do rozwiązywania układu równań nieliniowych mogą być używane dwie metody: przyrostowa i Arc-length.
Metoda przyrostowa
Jeśli w konstrukcji występują nieliniowe elementy (np. kable, podpory jednostronne, plastyczność materiałów), to obliczenia są automatycznie prowadzone przyrostowo.
W metodzie przyrostowej wektor prawej strony układu (wektor obciążenia) jest podzielony na „n” równych części zwanych przyrostami. Kolejny przyrost obciążenia jest przykładany do konstrukcji w momencie, gdy stan równowagi został osiągnięty dla poprzedniego przyrostu. Norma dla niezrównoważonych sił jest podawana dla każdego kroku, co pozwala śledzić zachowanie się relacji siła-przemieszczenie w konstrukcji.
Poniższy rysunek przedstawia przykład procesu nieliniowego wykorzystującego proces przyrostowy. Przedstawiono na nim wielkości wykorzystywane podczas obliczeń nieliniowych.
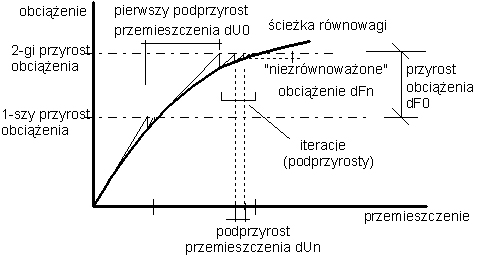
Przyrost obciążenia jest używany przy podziale obciążenia na mniejsze przedziały. Dla złożonych konstrukcji, w których wpływ efektów nieliniowych jest znaczny, obliczenia mogą nie być zbieżne, jeżeli analiza jest prowadzona dla wartości obciążenia przyłożonego w jednym kroku. Liczba przyrostów obciążenia ma wpływ na liczbę przebiegów obliczeń. Im większa liczba przyrostów, tym większe prawdopodobieństwo zbieżności obliczeń.
Metoda Arc-length
Metoda arc-length (sterowanie przemieszczeniem) powinna być stosowana, gdy przyrostowe algorytmy rozwiązywania równań poprzez sterowanie siłą nie są zbieżne.
Metoda Arc-length jest stosowana podczas nieliniowej analizy zniszczenia. Jest ona zalecana, jeśli są zdefiniowane nieliniowe atrybuty konstrukcji w modelu konstrukcji (zobacz załącznik).
Proces analizy
- Metoda pierwotnych naprężeń.
- Zmodyfikowana metoda Newtona-Raphsona.
- Kompletna metoda Newtona-Raphsona
Ogólnie, metoda pierwotnych naprężeń jest najszybsza, a kompletna metoda Newtona-Raphsona jest najwolniejsza. Jednak prawdopodobieństwo zbieżności jest większe przy pełnej metodzie Newtona-Raphsona niż w przypadku metody pierwotnych naprężeń.
W poniższej tabeli przedstawiono, w jaki sposób ustawić opcje aktualizacji macierzy, aby użyć odpowiedniego algorytmu.
| Algorytm | Aktualizacja macierzy po każdym podpodziale | Aktualizacja macierzy po każdej iteracji |
|---|---|---|
| Naprężenie pierwotne | Wyłącz | Wyłącz |
| Zmodyfikowana metoda Newtona-Raphsona | Włącz | Wyłącz |
| Kompletna metoda Newtona-Raphsona | Włącz | Włącz |
Użytkownik ma również możliwość użycia procedury modyfikacyjnej BFGS (Broyden-Fletcher-Goldforb-Shanno). Algorytm metody BFGS modyfikuje w trakcie obliczeń macierz sztywności. Dzięki użyciu algorytmu „line search” w niektórych przypadkach może nastąpić poprawa zbieżności metody.
Gdy zostanie osiągnięty stan równowagi, proces iteracji zostanie zatrzymany i będzie sprawdzana zbieżność procesu. Przyrosty przemieszczeń dUn i niezrównoważone siły dFn są wtedy równe zeru lub są mniejsze od zdefiniowanych dokładności dla obu wielkości. Proces iteracji zostaje zatrzymany, jeśli wystąpi rozbieżność. Brak zbieżności można zinterpretować jako numeryczny efekt spowodowany przeciążeniem konstrukcji. Może on być również spowodowany niestabilnością procesu numerycznego (np. gdy przyłożone obciążenie zostało podzielone na niewielką liczbę przedziałów). W takim przypadku liczba przyrostów obciążenia może zostać zwiększona w programie, co zazwyczaj pomaga w uzyskaniu zbieżności metody.
Patrz również:
Elementy prętowe w analizie nieliniowej dostępnej w programie Robot