Algorytm obliczania ugięcia płyt żelbetowych oparty jest na obliczeniach dla izotropowej płyty elastycznej wykonanej z elastycznego materiału. Brane są pod uwagę zmiany sztywności materiału spowodowane zarysowaniem. Pierwotnie przemieszczenia obliczane są z zastosowaniem Metody Elementów Skończonych (MES), następnie są one modyfikowane.
Obliczenia są przeprowadzane dla każdego panelu osobno. Takie założenie jest poprawne, gdy panel może być utożsamiony z elementem konstrukcyjnym (przęsłem, segmentem stropu), w przeciwnym wypadku wartości sztywności uśredniane w obrębie panelu mogą być zaburzone. Może to powodować wpływ bardzo oddalonych elementów na przemieszczenia analizowanego ES. Wpływ tego typu zaburzeń na wartości ekstremalne nie jest bardzo znaczący, jednak mapy deformacji (ugięć) należy traktować z dużą ostrożnością.
Zaleca się, aby każdy segment stropu, w którym mogą wystąpić lokalne ekstrema ugięć, był modelowany jako oddzielny panel. Panel ten powinien być zdefiniowany w granicach otaczających go podpór (podobnie jak przęsła w przypadku belek ograniczone są przez podpory). W przypadku panelu te podpory nie muszą być ciągłe na całym konturze panelu.
Podział na panele nie wpływa na wyniki weryfikacji metodą Z aktualizacją sztywności (MES) przy założeniu takich samych obciążeń, geometrii oraz wyliczonego zbrojenia.
Obliczenia są przeprowadzane dla wybranej kombinacji (odrębnej przemieszczenia dolnego i górnego) lub grupy kombinacji, o ile jest to wymagane przez normę (kombinacje częste, rzadkie i prawie stałe). Kombinacją wybraną do obliczeń jest ta, dla której występują maksymalne przemieszczenia sprężyste (odrębnie dodatnie i ujemne). W przypadku gdy panel nie może być traktowany jako element konstrukcyjny (zawiera w sobie więcej elementów konstrukcji), mapy deformacji (ugięć) należy traktować z dużą ostrożnością. Nie ma to jednak znaczącego wpływu na wartości ekstremalne ugięć dla danego panelu.
Należy zwrócić uwagę na przemieszczenia pozostałych podpartych naroży płyty.
Algorytm obliczeń użyty w programie Robot jest oparty na założeniu, że całkowite (rzeczywiste) ugięcia płyty żelbetowej równe są iloczynowi jej ugięć sprężystych oraz współczynnika sztywności D / B.
gdzie:
— rzeczywiste przemieszczenia i—tego punktu obliczeniowego płyty uwzględniające zarysowanie oraz obliczone zbrojenie
— sprężyste przemieszczenia i—tego punktu obliczeniowego płyty
D — sztywność płyty przy założeniu sprężystości materiału (jak w obliczeniach MES)
B — zastępcza sztywność płyty żelbetowej obliczona z uwzględnieniem zarysowania elementu, efektów reologicznych, przyczepności obliczonego zbrojenia itp. i uśredniona dla obu kierunków.
Takie podejście sprowadza się w praktyce do liniowego przeskalowania poszczególnych sprężystych przemieszczeń przez globalny współczynnik spadku sztywności.
Algorytm obliczeń dla metody sztywności zastępczej (sprężystej) jest następujący:
Po przeprowadzeniu analizy konstrukcji z wykorzystaniem MES i obliczeniu ilości zbrojenia teoretycznego dla stanu granicznego nośności, użytkowania (w zakresie obliczeń zarysowania, limitów naprężeń itp., czyli zagadnień, które mogą być rozpatrywane lokalnie) i wyjątkowego, w programie wyznaczane są sztywności dla każdego elementu skończonego (ES). Obliczenia sztywności przeprowadzane są dla dwóch kierunków zbrojenia. Zakres oraz sposób obliczania tych sztywności jest uzależniony od wymagań szczegółowych danej normy. W wyniku tych obliczeń uzyskujemy dwie wartości sztywności (w większości przypadków różne) dla każdego elementu skończonego. Do dalszych obliczeń wykorzystywana jest średnia ważona sztywności składowych. Wagą uśrednienia jest stosunek momentów działających na dany element w obu kierunkach.
gdzie:
Bx, By — sztywności rzeczywiste obliczone dla dwóch kierunków zbrojenia
cf — współczynnik wagowy, obliczony według wzoru:
- jeżeli | Mxx | / | Myy | > 4, to cf = 1
- jeżeli 0.25 ≤ | Mxx | / | Myy | ≤ 4, to
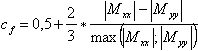
- jeżeli | Mxx | / | Myy | < 0.25, to cf = 0.
Powyższe wzory powodują, że w przypadku dużej dysproporcji momentów (stosunek momentu większego do mniejszego jest większy lub równy 4.0 — na przykład płyty zginane w jednej płaszczyźnie) brana jest pod uwagę sztywność z kierunku działania większego z momentów. Natomiast w przypadku, gdy wartości momentów są podobne, sztywność z danego kierunku jest przydzielana proporcjonalnie do stosunku momentów.
Kolejnym krokiem obliczeń jest wyliczenie stosunku sztywności sprężystej do uzyskanej we wspomniany sposób średniej ważonej sztywności rzeczywistych. Obliczenie to przeprowadzane jest dla każdego elementu skończonego.
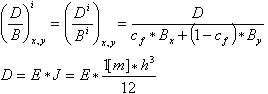
Współczynnik płytowy (1 — n*n) jest uwzględniany zarówno przy obliczeniach sztywności B i D.
Wartości uzyskanych w obliczeniach sztywności rzeczywistych można prześledzić włączając mapy Współczynnika sztywności.
Jeśli właściwości materiałów używanych podczas wymiarowania są identyczne do używanych w modelu, wtedy wartość współczynnika D / B > 1,0. Współczynnik ten można interpretować (głównie dla płyt zginanych w jednym kierunku) jako mnożnik ugięcia sprężystego. W przypadku użycia innych materiałów w modelu i obliczeniach (np. różnych klas betonu — betonów o innym module Younga lub Poissona), wartość współczynnika automatycznie jest korygowana, Może to spowodować zaburzenie przytoczonej wcześniej nierówności.
Kolejnym krokiem jest wyliczenie średniej z wyznaczonych wcześniej stosunków sztywności. Ostateczny, globalny stosunek sztywności, służący do obliczenia rzeczywistych przemieszczeń płyty (tzn. liniowego przeskalowania przemieszczeń sprężystych), jest liczbą uzyskaną z uśrednienia średniej stosunków sztywności (z wagą równą 0,25) oraz stosunku sztywności zarejestrowanego dla elementu, na którym występuje ekstremum momentu zginającego działającego w dowolnym kierunku (z wagą równą 0,75), według wzoru:
Algorytm metody sztywności zastępczej (sprężystej) zakłada uśrednienie sztywności dla wszystkich elementów skończonych; kształt linii ugięcia jest zatem identyczny z linią ugięcia przemnożoną przez współczynnik sztywności.
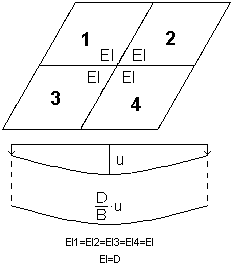
Algorytm metody z aktualizacją sztywności (niesprężystej) jest identyczny z algorytmem metody sztywności zastępczej (sprężystej) do momentu, gdy obliczona sztywność jest przypisywana niezależnie dla każdego elementu skończonego (różna dla kierunku X i dla kierunku Y). Uzyskujemy anizotropową płytę o zróżnicowanych sztywnościach. Dla tak przyjętych sztywności obliczane jest ugięcie płyty.
W metodzie z aktualizacją sztywności każdy element skończony posiada sztywność wyliczaną niezależnie, więc linie ugięcia mogą się różnić. Dla każdego elementu skończonego uzyskujemy inną sztywność dla każdego kierunku.
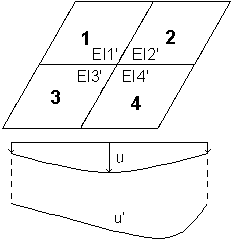
W przypadku włączenia opcji Korekta zbrojenia na karcie Parametry SGU w oknie dialogowym Typ zbrojenia płyt i powłok program podczas obliczeń zwiększa powierzchnię zbrojenia, aby zwiększyć sztywność elementu, co w konsekwencji prowadzi do ograniczenia ugięć płyty.
Zbrojenie jest rozkładane w obu kierunkach odwrotnie proporcjonalnie do sztywności. W przypadku, gdy nie jest możliwe ograniczenie ugięć poniżej dopuszczalnej wartości ugięcia określonej przez użytkownika (niemożliwa jest dalsza korekta zbrojenia z uwagi na dopuszczalny stopień zbrojenia), po zakończeniu obliczeń powierzchni zbrojenia teoretycznego pojawi się ostrzeżenie, że zostało przekroczone dopuszczalne ugięcie dla panelu.
W programie nie ma zdefiniowanych ograniczeń dotyczących zbrojenia innych poza normowymi; w związku z tym należy zwrócić uwagę na ekonomiczną poprawność rozwiązania. Należy zwrócić uwagę na to, że im bardziej ugięcie odbiega od wymaganego, tym mniejsza skuteczność stosowanej metody.