Dostępne rodzaje geometrii płyty

Lista rozwijana zawiera następujące typy geometrii płyt oraz parametry:

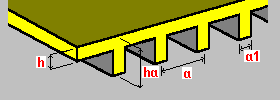
	Żebrowanie jednokierunkowe jednostronne: h — grubość płyty ha — wysokość żeber a — rozstaw żeber a1 — szerokość żeber
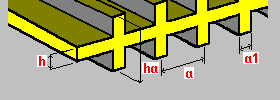
	Żebrowanie jednokierunkowe dwustronne: h — grubość płyty ha — wysokość żeber a — rozstaw żeber a1 — szerokość żeber
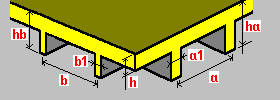
	Żebrowanie dwukierunkowe jednostronne: h — grubość płyty ha — wysokość żeber hb — wysokość żeber a — rozstaw żeber a1 — szerokość żeber b — rozstaw żeber b1 — szerokość żeber
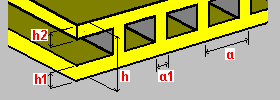
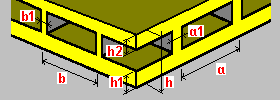
	Strop skrzynkowy jednokierunkowy: h — grubość stropu h1 — grubość płyty górnej h2 — grubość płyty dolnej a — rozstaw żeber a1 — szerokość żeber
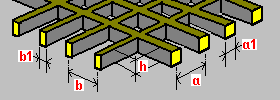
	Strop skrzynkowy dwukierunkowy: h — grubość stropu h1 — grubość płyty górnej h2 — grubość płyty dolnej a — rozstaw żeber a1 — szerokość żeber b — rozstaw żeber b1 — szerokość żeber
	Ruszt: h — wysokość żeber a — rozstaw żeber a1 — szerokość żeber b — rozstaw żeber b1 — szerokość żeber
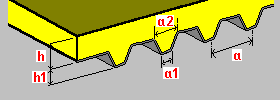
	Płyta na blasze trapezowej: h — grubość płyty h1 — wysokość blachy a — rozstaw żeber blachy a1 — szerokość dolna żeber a2 — szerokość górna żeber
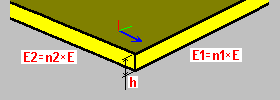
	Ortotropia materiałowa: h — grubość płyty n1 — współczynnik sztywności n2 — współczynnik sztywności
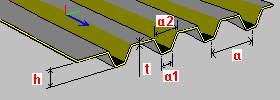
	Blacha trapezowa: h — wysokość blachy t — grubość blachy a, a1, a2 — wymiary pojedynczego segmentu blachy (rozstaw, szerokości)
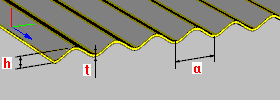
	Blacha falista: h — wysokość blachy t — grubość blachy a — wymiar pojedynczego segmentu blachy (rozstaw)
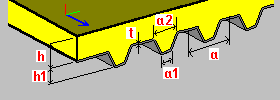
	Płyta zespolona z blachą trapezową h — grubość płyty h1 — wysokość blachy trapezowej t — grubość blachy a, a1, a2 — wymiary pojedynczego segmentu blachy (rozstaw, szerokości) Es — moduł Younga (stal trapezowa) vs — współczynnik Poissona (stal trapezowa) Eb — moduł Younga (beton; wartość przyjmowana na podstawie wybranego materiału) vb — współczynnik Poissona (beton; wartość przyjmowana na podstawie wybranego materiału)
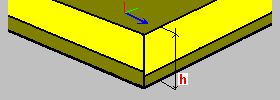
	Stała grubość ze zredukowaną sztywnością: h — grubość płyty współczynniki redukcji elementów macierzy: sztywności tarczowej D, sztywności giętnej K i sztywności ścinania H; dodatkowo może być zdefiniowany współczynnik redukcji ciężaru brany pod uwagę podczas generowania obciążenia ciężarem własnym; definiowanie wartości tych współczynników odbywa się w oknie dialogowym Współczynniki sztywności, ciężaru, masy, otwieranym po naciśnięciu przycisku Współczynniki.
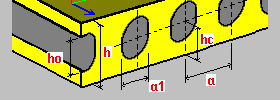
	Płyta kanałowa (z okrągłym lub owalnym otworem) h — grubość płyty a — rozstaw żeber, rozstaw otworów a1 — szerokość otworu / średnica okręgu ho — wysokość otworu (płyta z owalnymi otworami) hc — odległość między środkiem otworu i krawędzią płyty h1 — wysokość dolnej półki płyty h2 — wysokość górnej półki płyty (h2 = h — hc — c/2 — a1/2) c = ho — a1 (płyta z owalnymi otworami) Opcja Nie uwzględniaj sztywności zginania poprzecznego pozwala uniknąć uwzględniania sztywności zginania w obliczeniach K_YYYY. Nieuwzględnienie sztywności zginania (kierunek Y) ma na celu lepsze wymodelowania prefabrykowanych płyt kanałowych.

Ortotropia materiałowa wprowadza zróżnicowaną sztywność płyty spowodowaną różnymi własnościami fizycznymi w kierunkach prostopadłych. Różnica sztywności określona jest za pomocą zmodyfikowanych modułów Younga E1, E2, odpowiednio w wybranym kierunku ortotropii x, y. Moduły Younga E1, E2 są iloczynem modułu materiału wybranego w definicji i współczynników n1, n2 zdefiniowanych przez użytkownika. Współczynnik Poissona jest przyjmowany stały dla obu kierunków. Ortotropia tego typu może mieć zastosowanie na przykład do modelizacji płyt żelbetowych zbrojonych krzyżowo.

Współczynnik sztywności płyt żelbetowych krzyżowo zbrojonych można wyznaczyć na podstawie wzoru podanego poniżej. Zakładając, że materiał płyty jest liniowo sprężysty, współczynnik sztywności dla kierunku równoległego do kierunku zbrojenia wynosi:

n = 1+ 12/(h*h) * e*e * m * u / (1+ m*u)

gdzie:

h to wysokość przekroju płyty.

m = Ez/Eb – stosunek modułu Younga stali i betonu.

e to odległość środka ciężkości zbrojenia od płaszczyzny środkowej płyty.

u to procent zbrojenia (wyrażony w ułamku dziesiętnym), czyli pole przekroju prętów zbrojenia odniesione do jednostkowego pola przekroju płyty.

Patrz również:

Ortotropia — podstawy teoretyczne

Wzory na elementy macierzy ortotropowych