Użyj tego okna dialogowego, aby skonfigurować parametry solwera iteracyjnego.
- Dostęp
-
- Kliknij opcje Narzędzia
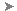Preferencje zadania. - Wybierz opcję Analiza konstrukcji w lewym panelu okna dialogowego Preferencje zadania.
- Wybierz opcję Iteracyjna, a następnie kliknij przycisk Parametry.
- Kliknij opcje Narzędzia
Elementy okna dialogowego
Typ solwera
Należy wybrać typ solwera:
- Wielopoziomowy wyłączony: PCGEBE
- Wielopoziomowy włączony: AEBEIS (zalecany)
Typy preconditionera:
Metody PCGEBE oraz AEBEIS opierają się na technice EBE z zastosowaniem następujących metod uwarunkowania wstępnego:
- Ukośnie: metoda Jacobiego
- Cholesky: uwarunkowanie symetryczne EBE Cholesky:
- Gaussa: uwarunkowanie symetryczne EBE Cholesky—Gauss—Seidel
- ICCF: niepełna faktoryzacja Cholesky'ego (zalecana)
Tolerancja
Definicja kolejnych iteracji (tolerancja) jest konieczna aż do spełnienia następującego warunku:
|| rk || / || b || ≤ tol
rk= b — K xk
Jako wektor normalny przyjęto maksimum Euklidesa i normalną. Na przykład:
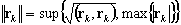
rk= wektor resztkowy
b= po prawej stronie (wektor obciążenia)
Xk — przybliżenie rozwiązania na k-tym kroku iteracji. Ten parametr określa precyzję iteracji. Jeśli przyjmiemy, że tol=0,001, to oznacza to, że co najmniej trzy pierwsze cyfry wartości reakcji będą takie same jak w rozwiązaniu ścisłym otrzymanym przy wykorzystaniu dokładnego solwera (metoda frontalna lub skyline). Zaleca się przyjmowanie tol=0,001 dla rozwiązania próbnego i tol = {1,0e-04 - 1.0e-08} dla rozwiązania ostatecznego.
Liczenie macierzy K
Jeżeli opcja Liczenie macierzy K jest włączona, to odpowiadające macierze dla elementów skończonych Ke (e € 1, Nele, gdzie Nele jest liczbą elementów skończonych w rozważanej konstrukcji) są obliczane za każdym razem, gdy obliczany jest iloczyn macierzy i wektora Kv;
Jeśli opcja Liczenie macierzy K jest wyłączona, to macierze elementów skończonych Ke (e Î 1, Nele) są brane z dysku.
Jest pomijana w przypadku podejścia ICCF, ale można z niej korzystać w przypadku następujących preconditionerów:
- Ukośnie
- EBE Gaussa
- EBE Cholesky
Parametry solwera wielopoziomowego
Należy zdefiniować liczbę poziomów agregacji. Domyślna wartość parametru zapewnia minimalną liczbę iteracji. Te złożone obliczenia wymagają więcej miejsca na dysku i czasu.
Zaleca się przyjęcie:
| Liczba równań | Liczba poziomów agregacji |
|---|---|
| < 20 000 | 1 |
| 20 000 — 50 000 | 2 |
| 50 — 200 000 | 3 — 4 |
| > 200 000 | 4 — 5 |
Należy pamiętać, że odpowiednio mały rozmiar problemu na zgrubnym poziomie (SPCL, small sized problems at the coarsest level) zapewnia szybkie iteracje. Z drugiej strony, im mniejszy SPCL, tym większa liczba iteracji.
Liczba wewnętrznych iteracji — opcja ta określa liczbę wewnętrznych iteracji podczas wygładzania. Wartość tego parametru zazwyczaj wynosi 3 lub 4. W pewnych przypadkach, mających zwykle miejsce podczas analizy dużych zadań, może zajść konieczność zwiększenia liczby wewnętrznych iteracji do 8.
Analiza przekątnej — włączenie tej opcji powoduje poprawienie agregacji poprzez analizę przekątnej macierzy sztywności K. Zaleca się włączenie tej opcji, aby przyspieszyć zbieżność.
Metody
Preconditionery ukośny, EBE Gaussa i EBE Cholesky'ego mogą wykorzystywać każdą z podanych metod. Przy podejściu ICCF zawsze używana jest Metoda 0.
Metoda 0 jest solwerem dwupoziomowym. Charakteryzuje się najszybszymi iteracjami w porównaniu z innymi metodami, Odznacza się najwolniejszą zbieżnością w odniesieniu do liczby iteracji.
Metoda 1 jest wielopoziomowym solwerem z ograniczonymi możliwościami wygładzania. To podejście zapewnia mniejsze wykorzystanie pamięci w porównaniu z Metodą 2; może być używane do rozwiązywania dużych problemów, jeżeli ze względu na możliwości komputera nie jest możliwe użycie Metody 2.
Metoda 2 jest wielopoziomowym solwerem z wykorzystaniem wygładzania na każdym poziomie agregacji. Charakteryzuje się najlepszą zbieżnością i pozwala na utrzymanie maksymalnej liczby poziomów agregacji. Prowadzi to do minimalnych wymagań związanych z pamięcią dyskową. Zaleca się używanie tej metody w przypadku, gdy liczba poziomów agregacji jest większa niż 2.
Zarządzanie pamięcią
Opcja Zarządzanie pamięcią określa wielkość bufora służącego do przechowywania macierzy elementów i elementów preconditionera. Ta opcja działa dla następujących typów uwarunkowania wstępnego: Diagonal, EBE Gauss i EBE Cholesky. W podejściu ICCF jest pomijana.
min: zapewnia minimalną wielkość bufora, ale może zmniejszyć szybkość obliczeń (ustawienie domyślne).
1/4: jedna czwarta pamięci systemowej przeznaczonej dla obliczeń.
1/2: połowa pamięci systemowej przeznaczonej dla obliczeń.
max: cała pamięć systemowa przeznaczona dla obliczeń.
Patrz również:
Parametry solwera iteracyjnego — informacje ogólne
Solwery dostępne w programie Robot
Zalecenie praktyczne dotyczące wyboru parametrów solwerów iteracyjnych