Solwery iteracyjne są używane w równaniach, kiedy metody zmiany kolejności dla solwerów bezpośrednich nie są efektywne, a macierz sztywności K jest wystarczająco dobrze uwarunkowana.
Informacje ogólne
Solwery iteracyjne są zalecane dla dobrze uwarunkowanych dużych problemów (15 000 – 1 000 000 równań), liniowych zadań statycznych i problemów wartości własnej (analiza modalna i analiza wyboczenia).
Tradycyjne metody bezpośrednie, czyli metoda frontalna, skyline i sparse, są czasochłonne i wymagają dużej ilości miejsca na dysku do przechowywania macierzy sfaktoryzowanej.
Solwery iteracyjne natomiast znacznie skracają czas obliczeń i mają mniejsze wymagania względem pojemności dysku. Należy jednak zwrócić uwagę na pewne wady solwerów iteracyjnych.
- Źle uwarunkowane problemy wolno osiągają zbieżność.
- Każdy przypadek obciążenia jest obliczany wielokrotnie od początku. Liczba zdefiniowanych przypadków powinna być jak najmniejsza.
Solwery iteracyjne są wydajne dla analizy konstrukcji zawierających bryłowe ES. Są one również przydatne podczas liniowej analizy statycznej (na przykład do wyszukiwania optymalnych parametrów projektu), kiedy możliwe jest uzyskanie przybliżonych rozwiązań dla kilku przypadków obciążenia.
Kontrola poprawności danych element po elemencie zgodnie z procedurą oszacowania Vinget stanowi dodatkowe zastosowanie solwerów iteracyjnych, umożliwiając wykrywanie problemów podczas znajdowania błędów w modelu ES.
Metoda gradientowa z uwarunkowaniem wstępnym (PCG) zawiera kilka typów uwarunkowań wstępnych.
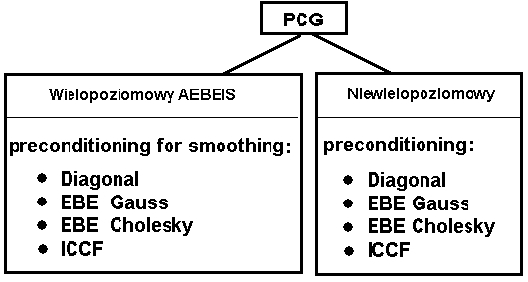
- AEBEIS: Agregacyjna metoda solwera iteracyjnego element po elemencie 1,2
- EBE: Element po elemencie
- ICCF: Podejście niekompletnego rozkładu Choleskiego
Element po elemencie (PCGEBE) i wielopoziomowy solwer iteracyjny (AEBEIS)
Solwer element po elemencie (PCGEBE) jest używany dla wszystkich typów elementów skończonych i nie posiada ograniczeń związanych z rozmiarem rozwiązywanego problemu. Jest natomiast wrażliwy na złe uwarunkowanie macierzy sztywności K — możliwa jest powolna zbieżność.
Wielopoziomowy solwer iteracyjny (AEBEIS) jest wielopoziomową, agregacyjną, iteracyjną procedurą rozwiązywania element po elemencie, która łączy w sobie zalety szybkich metod iteracyjnych z niedrogą techniką EBE. Pozwala przyspieszyć podstawowe operacje za pomocą niedrogich metod pod względem wymagań pamięci. Metody agregacyjne, takie jak ta, umożliwiają analizę brył i powłok (podobnie jak metody wielosiatkowe), jak również prętów i konstrukcji łączonych z prętów, powłok i brył.
Solwer AEBEIS zazwyczaj zapewnia szybszą zbieżność w porównaniu do metod niewielopoziomowych. Zapewnia stabilną zbieżność dla źle uwarunkowanych problemów, ale jest mniej bezpieczny. W rzadkich przypadkach uwarunkowanie wstępne jest zablokowane, ale zbieżność nadal przebiega wolno. Ten solwer powstał w wyniku połączenia solwera agregacyjnego w oparciu o technikę EBE.
Solwer AEBEIS umożliwia zastosowanie elementów prętowych 2D i 3D, elementów powłokowych (elementów 3-, 4-, 6- i 8-węzłowych) oraz elementów bryłowych. Pozwala ona również na dodatkowe elelementy składowe konstrukcji, takie jak podpory sprężyste, odsunięcia, zwolnienia i połączenia sztywne. Dla metody niewielopoziomowej nie ma ograniczeń dotyczących typów elementu lub konstrukcji.
Następujące typy uwarunkowania wstępnego są dostępne zarówno w AEBEIS, jak i w metodzie niewielopoziomowej.
- Diagonalna — uwarunkowanie wstępne Jacobiego (stosować tylko w przypadku dobrze uwarunkowanych problemów).
- EBE Gaussa — zmodyfikowane uwarunkowanie wstępne EBE Gaussa-Seidela-Choleskiego 12.
- EBE Choleskiego — uwarunkowanie wstępne EBE Choleskiego 34.
- ICCF: Podejście niekompletnego rozkładu Choleskiego 56.
Podejście ICCF jest szybsze od innych metod (diagonalnej, EPE Gaussa, EPE Choleskiego) i używa w przybliżeniu tej samej liczby iteracji, aby uzyskać konwergencję taką jak metody EPE Gaussa lub EPE Choleskiego. Nie wykorzystuje ono operacji I/O z dysku, ale zachowuje wyższ wymagania RAM. Podejście ICCF jest preferowane, jeśli komputer ma wystarczającą ilość pamięci RAM dla zadania. Pamięć RAM i wymagania dysku, jakich potrzebują metody EPE Gaussa i EPE Choleskiego są minimalne, ale są one wolniejsze niż podejście ICCF.