Podany poniżej przykład pokazuje, w jaki sposób należy definiować warunki kompatybilności w węzłach dla odpowiadających sobie przemieszczeń. Na poniższym rysunku pokazana jest przykładowa konstrukcja.
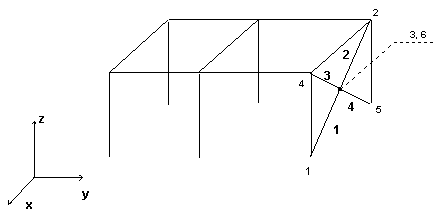
Dla tej konstrukcji zdefiniowano następujące węzły i pręty (patrz rysunek):
Węzły:
Nr 1 o współrzędnych (0, 0, 0).
Nr 2 o współrzędnych (2, 0, 2).
Nr 3 o współrzędnych (1, 0, 1). Węzły nr 3 i 6 mają identyczne współrzędne.
Nr 4 o współrzędnych (0, 0, 2).
Nr 5 o współrzędnych (2, 0, 0)
Nr 6 o współrzędnych (1, 0, 1). Węzły nr 3 i 6 mają identyczne współrzędne.
Pręty:
Nr 1 o początku w węźle 1, a końcu w węźle 3
Nr 2 o początku w węźle 3, a końcu w węźle 2; pręty numer 1 i 2 tworzą pierwszy pręt "I"
Nr 3 o początku w węźle 4, a końcu w węźle 6
Nr 4 o początku w węźle 6, a końcu w węźle 5. Pręty 3 i 4 zostają dodane tak, aby utworzyć drugi pręt "II".
Typ kompatybilności jest zdefiniowany w taki sposób, że przemieszczenia węzłów są takie same, a obroty w węzłach mogą być różne.
Kompatybilność węzła numer 3 i 6 ze względu na przemieszczenia UX, UY i UZ. Oznacza to, że pręty "I" i "II" mają te same przemieszczenia we wspólnym węźle 3 (6), natomiast ich obroty są różne. Taka definicja jest równoważna przegubowi pomiędzy dwoma ciągłymi prętami "I" i "II".