Konstrukcje cięgnowe są to takie konstrukcje, w których cięgno stanowi główny element nośny. Cięgnem nazywamy zaś element, w którym jeden z głównych wymiarów cięgna jest wielokrotnie większy od dwóch pozostałych wymiarów, a sztywność poprzeczna na zginanie i skręcanie jest niewielka w porównaniu ze sztywnością podłużną na rozciąganie.
Podstawowym wnioskiem z poprzedniej definicji jest to, że do cięgien mogą być zastosowane tylko siły rozciągające. Jednak w niektórych przypadkach niewielkie momenty zginania lub skręcania i siły ścinania mogą być zastosowane do cięgien. Główną zaletą struktury cięgnowej jest fakt, że cięgna charakteryzują się wysokimi dopuszczalnymi naprężeniami rozciągającymi.
Umożliwia to optymalne wykorzystanie przekroju cięgna, a co za tym idzie pozwala projektować konstrukcje lekkie, ekonomiczne i estetyczne. Korzystanie z cięgien w projektowanych konstrukcjach na dwie zalety:
- Wprowadzenie początkowego napięcia cięgna reguluje siły wewnętrzne i sprawia, że wyniki są bardziej efektywne.
- Łatwy montaż (na przykład podnoszenie i montowanie konstrukcji w całości – dzięki jej niewielkiemu ciężarowi).
W teorii konstrukcji kablowych przyjmowane są następujące założenia:
- Obciążenia i inne oddziaływania zewnętrzne mają charakter quasi—statyczny i nie zmieniają się w czasie
- Dla cięgien wiotkich brak jest momentów zginających i sił poprzecznych
- Elementy ciegien pracują w zakresie sprężystym (moduł Younga E = const)
- Cięgna mogą być obciążone dowolnym obciążeniem z wyjątkiem obciążenia momentem
- Dopuszczalne są duże przemieszczenia u, ale małe gradienty du / dx
- Powierzchnia przekroju cięgna F nie zmienia się (F=const)
- Długość cięgna nieobciążonego = l
Równania rządzące problemem
Rozpatrzymy wiotkie cięgno o małym zwisie (tzn. takie dla którego kąt między styczną w dowolnym punkcie cięgna i prostą łączącą jego końce jest mały), które zostało obciążone dowolnie rozłożonym obciążeniem w jego płaszczyźnie. Rozważmy nieskończenie mały elementu w tym cięgnie, który jest opisany w początkowym etapie (pierwszy etap – montaż) przez obciążenie q0, temperaturę T0 i naprężenie H0; długość tego elementu jest równa dso (Rys. 1a). Po przyłożeniu obciążenia (drugi, końcowy etap z obciążeniem q, temperaturą T i naprężeniem H), długość podstawowego przekroju cięgna jest równa ds (Rys.1b). Obydwa etapy razem z obciążeniami w obu płaszczyznach (xy i xz) przedstawiono również na rysunku 2.
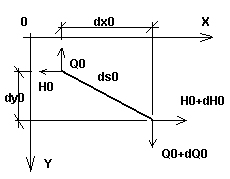 Rys.1a |
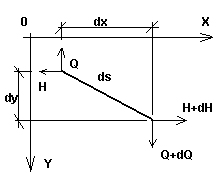 Rys.1b |
Wykorzystując założenie o małym zwisie cięgna oraz uwzględniając, że całkowita siła w cięgnie musi być skierowana wzdłuż stycznej do cięgna, można wyznaczyć odpowiednie wydłużenie elementarne odcinka cięgna w funkcji jedynie wielkości statycznych. Po scałkowaniu tej wielkości wzdłuż całej długości cięgna otrzymamy znaną postać równania wiotkiego cięgna o małym zwisie (1) określającą wielkość wydłużenia cięciwy cięgna D. Rys. 2 W powyższym równaniu przyjęto następujące oznaczenia:
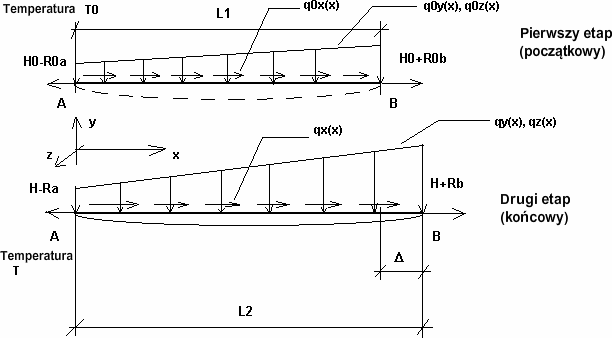
Rys. 2
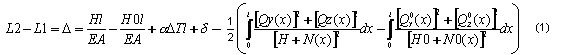
gdzie:
A, B — początkowy i końcowy węzeł cięgna,
EF – Sztywność cięgna na rozciąganie (E jest modułem Younga, a F przekrojem cięgna)
a — współczynnik rozszerzalności termicznej,
l — początkowa długość cięgna (dla cięgna nieobciążonego),
D — zmiana odległości pomiędzy podporami,
d — wstępne, wewnętrzne skrócenie/wydłużenie kabla (regulacja),
DT — zmiana temperatury,
Q(x) — funkcja zmiany siły poprzecznej jak dla swobodnie podpartej belki (w zależności od indeksów: odpowiednio w kierunku osi y i z oraz dla etapu początkowego lub końcowego) — schematyczny rysunek poniżej (rys. 3a), 3a.
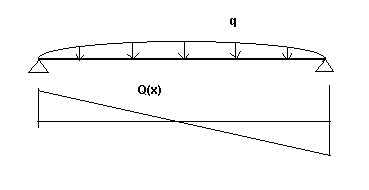
N(x)
N(x) – funkcja zmiany siły osiowej spowodowanej obciążeniem stycznym dla belki obustronnie utwierdzonej (dla etapu początkowego lub końcowego). Zob. Rys. 3b.
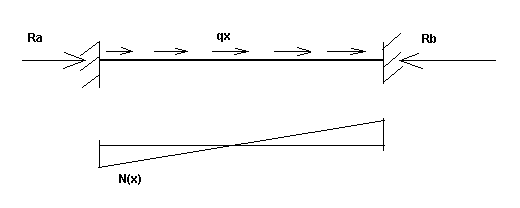
Rysunek 3b
Można jeszcze zauważyć, że w równaniu cięgna (1) w odróżnieniu od tradycyjnych rozwiązań stosowanych przy obliczeniach cięgien uwzględniono zmienność siły podłużnej na długości cięgna (w mianownikach obu funkcji podcałkowych w równaniu (1) występują składniki funkcyjne: [H+N(x)] 2 i [H0+N0(x)] 2 ). Dzięki temu uzyskuje się bardziej dokładne wyniki.
Patrz również:
Uwagi praktyczne dotyczące obliczania konstrukcji cięgnowych