Teoria elementu cięgnowego stosowanego w programie Robot jest oparta na ogólnej teorii wiotkiego cięgna rozciągliwego o małym zwisie. Zgodnie z tą teorią sztywność cięgna jest uwikłaną funkcją następujących parametrów: sztywności na rozciąganie (E*F), naciągu cięgna, przemieszczeń jego podpór, obciążenia poprzecznego w obu kierunkach (p y , p z ).
Należy zwrócić uwagę, że zdefiniowanie kabli w konstrukcji ze względu na nieliniowy charakter ich pracy powoduje konieczność wykorzystywania iteracyjnych metod analizy konstrukcji.
Możliwości stosowania cięgien w programie Robot:
- Cięgna mogą być stosowane razem z elementami następujących typów konstrukcji: RAMA PŁASKA, RAMA PRZESTRZENNA, POWŁOKA.
- Dopuszczalne są wszystkie standardowe typy analizy konstrukcji: liniowa (w rzeczywistości jest to analiza nieliniowa, z tym że nie są uwzględniane żadne inne efekty nieliniowe oprócz nieliniowości samych elementów kablowych), nieliniowa (uwzględnianie efektu naprężeniowego), P-Delta, przyrostowa, wyboczeniowa, dynamiczna, harmoniczna i sejsmiczna. Uwaga: Dynamiczne analizy jest traktowany jako liniowy w stosunku do bieżącej sztywność.
- Dopuszcza się stosowanie odsunięć.
- Materiał definiuje się tak jak dla pręta (wymagane jest podanie tylko modułu Younga E; w przypadku definiowania obciążenia ciężarem własnym cięgna należy podać dodatkowo ciężar właściwy CW, a w przypadku definiowania obciążenia termicznego współczynnik rozszerzalności termicznej ALFA)
- Kąty GAMMA definiuje się tak jak dla prętów (jest to istotne tylko przy opisie obciążenia).
Ograniczenia:
- Dla elementów cięgnowych nie jest możliwe definiowanie zwolnień ze względu na to, że nie posiadają one sztywności na zginanie i skręcanie.
Obciążenia cięgien
Do elementów kablowych można przykładać następujące rodzaje obciążeń:
- Obciążenia węzłowe
- Obciążenia stałe
- Obciążenie liniowe (stałe lub liniowo zmienne)
- Wstępne skrócenie/wydłużenie (dodatkowe obciążenie poza tymi określonymi podczas fazy montażowej)
- Obciążenie temperaturą
- Obciążenie siłami skupionymi na długości elementów.
Nie są dozwolone następujące rodzaje obciążenia elementów kablowych:
- Moment
- Obciążenie momentem rozłożonym
SKŁADNIA (dane wpisywane przez użytkownika w pliku tekstowym)
CHArakterystyki
(<lista elementów>) kabli AX= <Powierzchnia przekroju> (E= <moduł Younga>)
Szerokość (RO= <jednostki>) [naprężenie = <Y>|siła = <h>|długość = <M>
| [ DILatation = <D> (względne) ]]
gdzie:
NAPrężenie — naprężenie normalne (liczone w odniesieniu do cięciwy cięgna), które ma być osiągnięte dla obciążeń przypadku montażowego.
SIŁa — siła naciągu (liczona w odniesieniu do cięciwy cięgna), która ma być osiągnięta dla obciążeń przypadku montażowego.
DŁUgość — długość cięgna w stanie nieobciążonym.
DYLatacja — różnica długości cięgna w stanie nieobciążonym i odległości węzłów pomiędzy którymi cięgno jest zamocowane (jeśli jest to wartość dodatnia, to długość cięgna jest większa od odległości między węzłami, a jeśli ujemna, to odległość między węzłami jest większa od długości cięgna)
DYLatacja WZGlędna — stosunek różnicy długości cięgna w stanie nieobciążonym i odległości węzłów pomiędzy którymi cięgno jest zamocowane do odległości węzłów pomiędzy którymi cięgno jest zamocowane (jeśli jest to wartość dodatnia, to długość cięgna jest większa od odległości między węzłami, a jeśli ujemna, to odległość między węzłami jest większa od długości cięgna).
- Moduł Younga E może być deklarowany w definicji materiału.
- Słowa kluczowe: naprężenia, siły, długość i DILatation są wyraźnie zdefiniowane i nie są wymagane. Jeśli żaden z tych parametrów są określone, początkowa długość kabla jest równa odległości między węzłami.
Montażowy przypadek obciążenia cięgna
Program Robot posiada funkcję projektowania montażowego konstrukcji. Zalecane jest, jest to pierwszy Przypadek obciążenia. Poniżej podano składnię tego przypadku obciążenia:
PRZypadek
MONtaż
[opis obciążeń]
Dla tego przypadku obciążenia:
- We wskazanych prętach panują siły wstępnego naciągu o wartości określonej przez użytkownika poprzez podanie jednej z dwóch poniższych wartości w składni pliku tekstowego (polecenie CHArakterystyki):
NAPrężenie = s0 (wstępne naprężenie kabla) lub
SIŁa = t0 (wstępna siła naciągu w kablu),
- Można określić początkową długość cięgna nie napiętego i nie obciążonego podając DŁUgość = l
0
, jeśli ma być ona różna od przyjmowanej domyślnie wartości LONG =
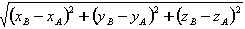 równej odległości pomiędzy węzłami.
równej odległości pomiędzy węzłami. - Można określić wstępne skrócenie/wydłużenie cięgna za pomocą polecenia DYLatacja (WZGlędna).
- Jeśli nie występuje słowo kluczowe WZGlędna, DYLatacja jest podawana w wartościach bezwzględnych.
- Jeśli występuje słowo kluczowe WZGlędna, wstępne wydłużenie podawane jest w postaci względnej, tzn. końcowa długość cięgna będzie równa L = LONG (1 + DYL).
- Ddziałają wszystkie zdefiniowane przez użytkownika obciążenia (np. ciężar własny, dodatkowe masy).
- Można zdefiniować temperaturę TX dla cięgien będących w fazie montażu.
- Przemieszczenia wyznaczone dla tego przypadku obciążenia określają wyjściową geometrię dla pozostałych przypadków analizy konstrukcji.
Podczas analizy kolejnych przypadków obciążenia konstrukcji w warunkach równowagi uwzględniane są obciążenia przyłożone w przypadku montażowym. Przemieszczenia wyznaczone dla tego przypadku traktowane są jako wyjściowe. Siły naciągu, które wstępnie zostały zdefiniowane, ulegają zmianie (oznacza to, że po montażu cięgna zostają zakotwione).
Postać równania cięgna wiotkiego dla etapu montażowego
W tym etapie równanie (1) opisuje przejście od:
- Cięgno nieobciążone („cięgno leżące na ziemi”):
q0x = q0y = q0z = 0 (brak obciążenia)
H0 = 0 (brak naciągnięcia kabla)
T0 = 0
dla którego długość jest równa L1= :
1.
long, gdy (long ≠ 0) – ma to miejsce, jeżeli w definicji cięgna podawana jest wartość DŁUgości
2.
[odległość (A, B) + dylatacja], gdy dylatację definiujemy w układzie absolutnym — ma to miejsce, jeżeli w definicji cięgna podawana jest wartość DYLatacji
3.
[odległość (A, B)*(1+dylatacja)], gdy dylatację podajemy w układzie relatywnym — ma to miejsce, jeżeli w definicji cięgna podawana jest wartość DYLatacji WZGlędnej
4.
[odległość (A, B)], gdy (dylatacja = 0) i (long = 0) — ma to miejsce, jeżeli w definicji cięgna nie wystąpiło żadne z wymienionych słów kluczowych: DŁUgość, DYLatacja i DYLatacja WZGlędna lub występuje jedno ze słów kluczowych: SIŁa lub NAPrężenie.
aby
- Cięgno zamontowane w konstrukcji ze wszystkimi obciążeniami pierwszego (montażowego) przypadku obciążenia:
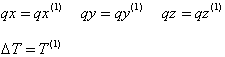
L2 jest odległością pomiędzy węzłami zamocowania A i B odkształconego cięgna:
L2 = odległość (A+U A , B+U B ),
gdzie:
U A — przesunięcie punktu A
U B — przesunięcie punktu B.
Możliwe są różne przypadki pierwszego, montażowego przypadku obciążenia:
- Siła H jest znana (kontrolowana) — gdy NAPrężenie lub SIŁa (naciągu) są różne od zera (NAPrężenie≠0 lub SIŁa≠0). Wtedy siła naciągu jest równa:
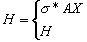
Z równania (1) otrzymujemy:
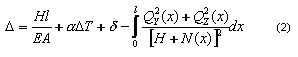
Wartość l przyjmowana jest jako odległość początkowego i końcowego węzła cięgna.
Z równania (2) możemy wyznaczyć wstępne wydłużenie cięgna d potrzebne do uzyskania wymaganej siły H:
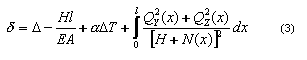
- Siła naciągu H nie jest znana (w definicji składni cięgna nie jest podana wartości ani NAPrężenia, ani SIŁy), to wtedy:
- Gdy weźmiemy pod uwagę przemieszczenia podczas fazy montażowej (zdefiniowane przez podanie w skrypcie kabla wartości DŁUgości, DYLatacji lub DYLatacji WZGlędnej), tzn.
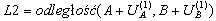
to rozwiązując równanie (4) ze względu na siłę H
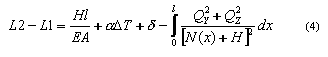
i iterując cały układ równań otrzymujemy końcową wartość siły montażowej.
Końcowa wartość siły będzie równa:
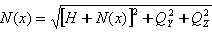 .
. - Jeżeli nie weźmiemy pod uwagę przemieszczenia węzłów, tzn.
L2 = odległość (A, B),
rozwiązując równanie (4) otrzymujemy wstępną wartość siły potrzebną do zakotwienia kabla pomiędzy podporami.
- Gdy weźmiemy pod uwagę przemieszczenia podczas fazy montażowej (zdefiniowane przez podanie w skrypcie kabla wartości DŁUgości, DYLatacji lub DYLatacji WZGlędnej), tzn.
- Siła H jest znana (kontrolowana) — gdy NAPrężenie lub SIŁa (naciągu) są różne od zera (NAPrężenie≠0 lub SIŁa≠0). Wtedy siła naciągu jest równa:
Przypadki obciążenia cięgna po jego zakotwieniu
Po zakończeniu obliczeń konstrukcji wyniki otrzymywane dla elementów kablowych są podobne do tych uzyskiwanych dla elementów prętowych; istnieją jednak różnice pomiędzy tymi dwoma typami wyników. Poniżej omówiono te różnice:
- Dla elementów cięgnowych nie można uzyskać wykresów momentów i sił poprzecznych,
- Dla elementów cięgnowych można uzyskać deformację uproszczoną wyznaczoną jak dla pręta kratownicy lub dokładną określoną na podstawie równania różniczkowego krzywej zwisu
- Dla elementów cięgnowych pojawiają się dodatkowe wyniki wynikające ze stanu montażowego:
- W cięgnach, gdzie wymagany jest żądany naciąg (w składni programu Robot: NAPrężenie lub SIŁa), wyznaczana jest wielkość regulacji [m] niezbędnej do uzyskania wymaganego naciągu
- W innych kabli, siły niezbędne do assemblage jest przypisana
Takie wyniki są przydatne podczas projektowania zespołu. Są dostępne w module Wyniki poprzez wybranie polecenia Naprężenia > Parametry > Wyniki dla elementów kablowych na etapie montażowym.
- Siła osiowa (rozciągająca) jest wyznaczana ze wzoru:
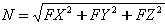
gdzie:
N — siła działająca wzdłuż stycznej do cięgna
FX, FY, FZ — siły składowe siły N zrzutowane na kierunki poszczególnych osi lokalnego układu współrzędnych cięgna.
Postać równania cięgna wiotkiego w trakcie pracy cięgna w konstrukcji
W przypadku dowolnego przypadek (i) są definiowane po pierwszym tworzeniu przypadku kabli zachowanie uzyskuje się przez zakończenie równanie (1). Iteracja takie równanie jest uruchamiane zgodnie z następujące założenia:
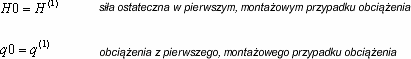
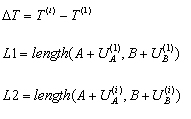
![]() Obciążenie z pierwszego przypadku obciążenia jest automatycznie dodawane do obciążenia w przypadku (i)
Obciążenie z pierwszego przypadku obciążenia jest automatycznie dodawane do obciążenia w przypadku (i)
Siła naciągu H jest niewiadomą.
Patrz również:
Uwagi praktyczne dotyczące obliczania konstrukcji cięgnowych