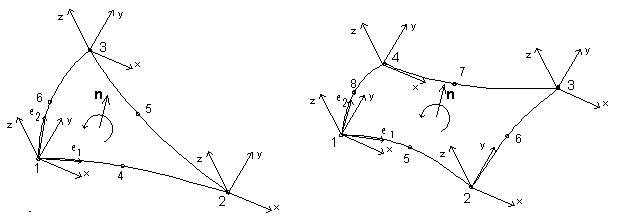
Znajomość lokalnego układu współrzędnych dla powierzchniowego elementu skończonego nie jest konieczna, gdyż każdy węzeł takiego elementu posiada własny, lokalny układ współrzędnych. Ważne jest jednak, aby znany był kierunek wektora normalnego do powierzchni elementu skończonego (najlepiej jednakowy dla wszystkich elementów), gdyż w przeciwnym razie definicja obciążenia na elemencie (np. ciśnienia prostopadłego do powierzchni elementu powłokowego) może być niepoprawna.
Kierunek wektora normalnego (prostopadłego do powierzchni elementu skończonego) ustalany jest zgodnie z regułą śruby prawoskrętnej (w kierunku od pierwszego do ostatniego węzła elementu). Lokalne układy współrzędnych oraz zwrot wektora normalnego do elementu pokazano na poniższym rysunku; jako przykład wybrano 6—cio i 8—mio węzłowe elementy skończone.
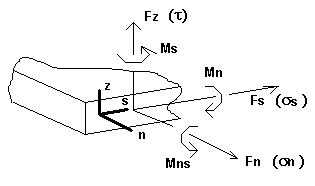
Dla powierzchniowych elementów skończonych uzyskiwane są siły i naprężenia w elemencie. Są one określane na podstawie położenia w stosunku do lokalnego kierunku normalnego i stycznego do przekroju poprzecznego. Przyjęto następującą konwencję znakowania:
- n — wektor, który jest prostopadły do powierzchni elementu przekroju
- e — wektor, który jest styczny do powierzchni elementu przekroju
- z — wektor prostopadły, zewnętrzny do powierzchni elementu.
Wektory te tworzą układ współrzędnych kartezjańskich podlegający regule śruby prawoskrętnej. Dodatnie kierunki sił, momentów i naprężeń działających w danym przekroju poprzecznym definiowane są zgodnie z kierunkami wektorów n, s, z. Opisana powyżej konwencja jest schematycznie przedstawiona na poniższym rysunku. Siły, momenty oraz naprężenia pokazane na rysunku mają dodatnie znaki.
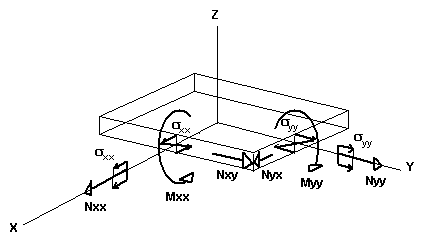
Wyniki otrzymane dla powierzchniowych elementów skończonych są przedstawiane w lokalnych układach współrzędnych, które mogą być definiowane i zmieniane przez użytkownika w dowolnym momencie prezentowania wyników. Przykładowo dodatnie kierunki sił i odpowiadających im naprężeń w węźle przedstawiono poniżej na rysunku dla osi X jako kierunku odniesienia.
Zobacz także: