Analiza modalna z uwzględnieniem sił statycznych — opis i przykład

Siły statyczne przyłożone do konstrukcji mają wpływ na częstotliwość drgań własnych konstrukcji. Używana powszechnie analiza modalna (wyznaczanie drgań własnych konstrukcji) nie bierze pod uwagę wpływu sił statycznych; Aby zbliżyć się do realnych warunków pracy konstrukcji, w obliczeniach przeprowadzanych w programie Robot może zostać wykorzystana analiza modalna z uwzględnieniem przyłożonych sił statycznych.

Obliczenia drgań własnych konstrukcji z uwzględnieniem działania sił statycznych przeprowadzane są w dwóch etapach: Liniowa (1) lub nieliniowa (2) analiza statycznego związku naprężenia-odkształcenia pod wpływem zadanego obciążenia statycznego.

Etap pierwszy — analiza liniowa:

gdzie:

x_st — nieznany wektor stanu statycznego

b — wektor zadanego obciążenia statycznego (wektor obciążenia statycznego)

K — macierz sztywności

L (x_st, b) — operator nieliniowy.

Wektor obciążenia statycznego b może być prostym przypadkiem obciążeniowym lub kombinacją zdefiniowanych przypadków obciążeniowych.

Etap drugi — analiza nieliniowa:

, ( 2a )

gdzie:

K_s — macierz sztywności naprężeniowej wywołana naprężeniami ze stanu statycznego

M — macierz mas

ω_i² — wartość własna (ω_i = pulsacja)

Φ — wektor własny

Do rozwiązywania nieliniowego problemu statycznego (2) stosowane są te same metody jak w nieliniowej analizie statycznej. Dla liniowego problemu statycznego zachodzi korelacja: , gdzie G jest macierzą sztywności geometrycznej.

Dodatnie wartości ω_i (ω i > 0) opisują stabilne stany równowagi, wartości ujemne (ω_i < 0) — niestabilne stany równowagi, Natomiast wartość zerowa (ω_i = 0) oznacza brak stabilności (wyboczenie).

Jeżeli macierz K + K_s (x_st) przestaje być dodatnio określona, to oznacza to, że obciążenie statyczne jest bliskie (przystaje do) wartości krytycznej (wyboczeniowej). W trakcie analizy nieliniowego problemu statycznego (2) zbieżność nie zostanie osiągnięta. Jeżeli wybrane zostało podejście liniowe (etap analizy statycznej) i macierz nie jest dodatnio określona (pojawia się na ekranie komunikat ostrzegający o tym fakcie), to zaleca się przerwanie obliczeń, gdyż dalsze obliczenia nie mają sensu.

Uwaga: Jeżeli w konstrukcji występują elementy kablowe lub elementy typu rozciąganie-ściskanie, w programie dostępne jest jedynie podejście nieliniowe.

Przykład

Rozważmy przykładową konstrukcję pokazaną na poniższym rysunku. N oznacza obciążenie statyczne.

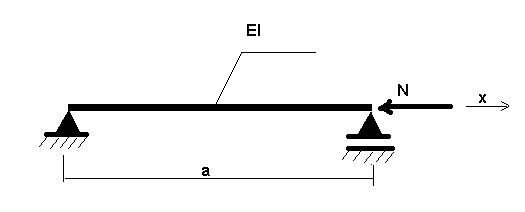
Przedstawione poniżej równanie opisuje zachowanie pokazanej na powyższym rysunku konstrukcji.

, ( 3 )

gdzie:

w — przemieszczenia spowodowane zginaniem

ρ — gęstość materiału

F — pole przekroju poprzecznego.

Rozwiązanie tego równania będzie poszukiwane w postaci:

( 4 )

Po podstawieniu wyrażenia ( 4 ) do ( 3 ) otrzymujemy:

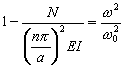, ( 5 )

gdzie:

— obciążenie wyboczeniowe

ω₀² — wartość własna dla N=0 (wynik zwykłej analizy modalnej).

Po przekształceniach tego wzoru ostatecznie otrzymujemy:

, ( 6 )

gdzie ω² — wartość własna uzyskana dla konstrukcji poddanej działaniu obciążenia statycznego N.

Wynik rozważań jest przedstawiony graficznie na poniższym rysunku.

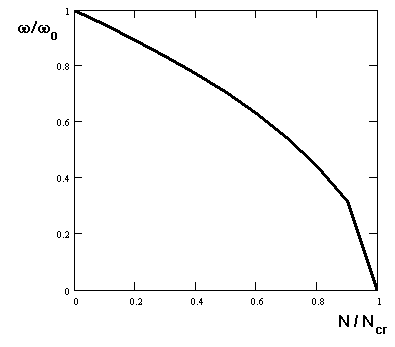
Na zakończenie należy stwierdzić, że dla rzeczywistych konstrukcji zależność ω = ω(b) jest zazwyczaj nieco bardziej skomplikowana niż ta, która wynika ze wzoru (6).