Analiza modalna służy do wyznaczania wartości własnych i ich wielkości pochodnych (częstości własne, częstotliwości własne lub okresy własne), precyzji, wektorów własnych, współczynników udziału i mas uczestniczących dla zagadnienia drgań własnych konstrukcji.
W programie dostępne są trzy tryby dynamicznej analizy konstrukcji: modalny, sejsmiczny oraz sejsmiczny pseudomodalny.
Wartości i formy własne konstrukcji są wyznaczane z następującego równania:
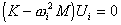(1)
gdzie:
K — macierz sztywności konstrukcji,
M — macierz mas konstrukcji,
ωi — częstość własna (częstość własna kołowa) formy "i",
Ui — wektor formy własnej "i".
Liczba form własnych wyznaczanych w programie może być określona poprzez:
- górną granicę częstości, częstotliwości lub okresu
- dolną granicę sumy mas uczestniczących (wyrażonych w procentach), albo wprost jako liczba wymaganych form.
Jeśli liczba form nie jest podana, to w obliczeniach przyjmowana jest wartość domyślna liczby form określona w Preferencjach.
Następujące parametry sterują rozwiązaniem problemu własnego:
- dokładność obliczeń (wielkość dopuszczalnego błędu),
- maksymalna liczba iteracji.
W programie dostępne są następujące rodzaje macierzy mas:
- rozłożona (macierz pełna — zawsze uwzględnia obrotowe stopnie swobody),
- Skupiona z rotacjami (macierz diagonalna, w której uwzględnione są obrotowe stopnie swobody),
- Skupiona bez rotacji (macierz diagonalna bez uwzględniania obrotowych stopni swobody).
Skupione macierze mas Mlum są tworzone zgodnie z następującą zasadą:
Mlum(i,j) = 0.0 ; dla i≠j
Mlum(i,j) = Stot/Sdiag * M(i,j) ; dla i=j (2)
gdzie:
Stot — suma wszystkich elementów pełnej macierzy mas M,
Sdiag — suma elementów leżących na przekątnej głównej w macierzy mas M.
Z podanych definicji wynika, że macierz elementu jest zachowana i dodatnio określona.
Wektory własne pokazywane w wynikach obliczeń są normalizowane w taki sposób, że maksymalna składowa każdego wektora jest równa 1.0.
Wektory własne używane podczas obliczeń są normalizowane w taki sposób, że:
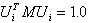(3)
Wartość precyzji podawana w oknie wartości własnych oznacza uzyskaną dokładność zbieżności. Wartość ta jest miarą błędu, z jakim wartość własna λ i oraz wektor własny Ui wyznaczone podczas iteracji dla i—tej formy spełniają podane poniżej równanie problemu własnego:
K * Ui = λi * M * Ui (4)
Współczynniki udziału są zdefiniowane w następujący sposób:
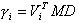
gdzie:
D — wektor jednostkowy zdefiniowany w podany poniżej sposób:
D(j) = 1.0, jeśli "j" odpowiada i—temu stopniowi swobody
D(j) = 0.0, jeśli j ¹ i
Vi — wektor formy własnej "i" znormalizowany w taki sposób, że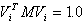 
Masy uczestniczące są masami dynamicznymi biorącymi udział w ruchu konstrukcji dla każdej formy własnej i każdego stopnia swobody. Są one przedstawiane jako bieżące masy dla aktualnej formy własnej i jako względne masy będące sumą mas bieżących od pierwszej do bieżącej formy. Wartości są wyświetlane w procentach całkowitych mas dynamicznych.
Bieżące masy uczestniczące są zdefiniowane w następujący sposób:
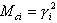
Obecnie domyślną metodą rozwiązywania problemu własnego jest metoda Lanczosa, która jest doskonałym algorytmem umożliwiającym rozwiązywanie dużych problemów wartości własnych (1). To podejście pozwala na uzyskanie poszukiwanych pierwszych „n" wartości i wektorów własnych z dowolną dokładnością.
Dla większości problemów najbardziej polecaną metodą ze wszystkich metod dostępnych w systemie Robot jest metoda Lanczosa. Ten algorytm posiada jednakże poniższe ograniczenia:
- Macierz trójdiagonalna T nie powinna być rozłożona.
- Macierz mas M powinna być traktowana jako Skupiona z rotacjami lub Rozłożona. Jeśli wybrana jest opcja Skupiona z rotacjami, macierz mas jest automatycznie definiowana jako Skupiona z rotacjami.
Gdy w programie wybrana zostanie metoda Lanczosa, to program automatycznie zmieni metodę obliczeń na metodę iteracji podprzestrzennej. Jeżeli koniecznie chcemy użyć w obliczeniach metodę Lanczosa, to należy tak połączyć konstrukcje rozłączne, aby nie został zmieniony model konstrukcji (np. dodać pręt pomiędzy podporami).
Metoda Lanczosa wykorzystuje przedstawioną poniżej redukcję trójdiagonalnej macierzy T
gdzie
Qj = {q1, q2,..., qj}— macierz prostokątna Neq x j, Neq jest liczbą równań, j — liczbą "kroków" Lanczosa, qj — j—ty wektor Lanczosa.
Wyrażenie
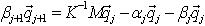
pozwala utworzyć kolejny wektor Lanczosa qj+1 oraz podać aktualną linię macierzy T
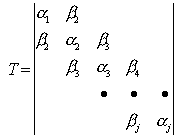
Stąd otrzymujemy zredukowany problem własny:
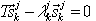, k=1,2,…,j
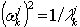, gdzie ωk j jest j-tym przybliżeniem ωk, k=1,2,..., n, i n jest wymaganą liczbą wartości własnych i wektorów własnych. Algorytm będzie kontynuował obliczenia (zwiększając j — liczbę kroków Lanczosa), aż do uzyskania odpowiedniej dokładności dla wszystkich "n" wartości własnych.
Procedura ortogonalizacyjna zapewnia ortogonalność pomiędzy wektorami Lanczosa qj, co oznacza bezpieczeństwo i numeryczną stabilność procesu obliczeniowego.
Wektory własne są wyznaczane z poniższych równań:
U = Qs
Metoda redukcji bazy
Metoda redukcji podstawowej pozwala na uzyskanie przybliżonych wielkości kilku pierwszych wartości własnych, jeżeli dostępne są dla nich pewne dane. Metoda wymaga zdefiniowania stopni swobody typu „master" (MDOF — „master degree of freedom") w celu uzyskania układu zredukowanego. Zatem użytkownik ma możliwość rządzenia procesem tworzenia modelu zredukowanego. Jest to bardzo dobre narzędzie dla użytkowników, którzy mają pewne doświadczenie w prowadzeniu analizy dynamicznej konstrukcji oraz gdy znane jest zachowanie dynamiczne projektowanej konstrukcji. Metoda pozwala wykluczyć niepotrzebne stopnie swobody ze zredukowanego modelu, co prowadzi do znacznie mniejszego układu po usunięciu tych stopni swobody.
Metoda posiada następujące cechy:
- Podane muszą być MDOF: węzły i kierunki typu "master". Zakłada się, że tylko przemieszczenia (a nie obroty) mogą być przyjęte jako stopnie swobody typu „master”,
- Algorytm może wykorzystywać dowolny typ macierzy mas, Jednak najkrótszy czas obliczeń będzie uzyskany w przypadku użycia macierzy mas Skupiona bez rotacji.
- Weryfikacja Sturma będzie wskazywała liczbę pominiętych częstotliwości. Nie będzie próbowała znaleźć tych wartości i wektorów własnych. Istnieje tylko jedna metoda, aby sprawdzić zbieżność weryfikacji: zwiększenie liczby MDOF, aby rozwiązać ten problem oraz porównać wartości własne.
Metoda wykorzystuje transformację dużego problemu własnego dla modelu MES.
K U — ω 2 M U = 0 do problemu własnego dla zredukowanego modelu:
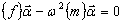
gdzie {f} — macierz wpływu, \{m\} — uogólniona macierz mas dla modelu zredukowanego.
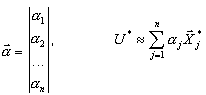
Bazą dla takiej transformacji są rozwiązania otrzymane dla odpowiednich stanów jednostkowych:
jednostkowe siły węzłowe są przykładane kolejno do każdego węzła typu "master" w wybranym kierunku typu "master". Duże zadanie statyczne zostanie rozwiązane dla "n" prawych stron:
K Xi * = Ti , i = 1, 2, …, n
gdzie Ti — wektor obciążenia odpowiadający i—tej sile jednostkowej. Użytkownik musi zdefiniować węzły i kierunki typu ‘master’. Wszystkie pozostałe operacje będą wykonywane poprzez program. Zredukowany problem własny jest następnie rozwiązywany przy użyciu metody Jacobiego. W rezultacie uzyskiwane są przybliżone wartości częstotliwości wi i wektorów własnych Ui *, i=1,2,..., n.
Zobacz także:
Analiza modalna — Dokładność obliczeń w analizie modalnej konstrukcji