Obliczanie jakości trójkątów jako oczek siatki
Przy generowaniu siatki trójkątnej należy dążyć do takiej siatki, aby jej oczka, czyli wygenerowane trójkąty, były trójkątami równobocznymi. Każdy inny trójkąt, a w szczególności trójkąt rozwartokątny jest "gorszym" oczkiem siatki z punktu widzenia Metody elementów skończonych (MES).
Przyjmując, że współczynnik jakości elementów siatki trójkątnej zawiera się w przedziale <0,1>, przyjmujemy, że współczynnik α jest równy 1 dla trójkąta równobocznego.
Współczynnik α dla trójkąta o wierzchołkach ABC wyznaczamy ze wzoru:
Algorytm opiera się na obliczaniu iloczynu wektorowego dwóch wektorów w przestrzeni.
Obliczanie jakości czworokątów jako oczek siatki
Postępujemy podobnie biorąc pod uwagę, że idealnym czworobokiem jest prostokąt. Do wyznaczania współczynnika α stosowana jest metoda obliczania współczynników trójkątów.
Dowolny czworokąt ABCD dzielimy na cztery nakładające się trójkąty: ABC, ACD, ABD, BCD. Obliczenia współczynników α wykonywane są dla poszczególnych trójkątów: { α1, a2, α3, α4} = { α (ABC), α (ACD), α (ABD), α (BCD)}. Mając obliczone te współczynniki obliczamy współczynnik jakości czworokąta.
temp1 = α1 * α3;
temp2 = α2 * α4;
if( temp1 * temp2 != 0 )
α= ( temp1 > temp2 ) ? temp2 / temp1 : temp1 / temp2;
α_rect = 0.86602540000000;
α_avg = (α_rect — fabs((α1 + α2 + α3 + α4) / 4. — α_rect))/ α_rect;
Jeśli (α_avg < α) α= α_avg;
Obliczanie globalnego współczynnika jakości siatki
Mamy dwa sposoby obliczania globalnego współczynnika:
- Wartości jakości wszystkich elementów (trójkątów, czworokątów) siatki zostają uśrednione.
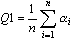
gdzie n — ilość oczek siatki
- Wartości jakości ważonej wszystkich elementów (trójkątów, czworokątów) siatki zostają uśrednione, przy czym wagą jest powierzchnia elementu siatki.
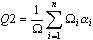
gdzie n — numer elementu siatki, Ω — powierzchnia