Informacje na temat metody blokowej iteracji podprzestrzennej

Metoda blokowej iteracji podprzestrzennej służy do rozwiązywania uogólnionego problemu własnego.

Uogólnione problemy własne spotykane są w modalnej lub wyboczeniowej analizie konstrukcji.

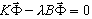
Uogólniony problem własny (1)

Gdzie:

• K — macierz sztywności.
• B = M — macierz mas w przypadku analizy dynamicznej; w pozostałych przypadkach B = Ks, gdzie Ks oznacza macierz sztywności naprężeniowej wywołaną linearyzacją odpowiedniego operatora nieliniowego w przypadku analizy wyboczeniowej.
• λ — wartość własna.
• Φ — wektor własny.

Metoda blokowej iteracji podprzestrzennej jest zalecana w przypadkach, gdy dla konstrukcji należy uzyskać znaczną liczbę par własnych (wartości i wektorów własnych). Zazwyczaj jest to więcej niż 10.

Uwaga: Metoda blokowej iteracji podprzestrzennej może zostać zastosowana do konstrukcji rozłącznych.

Metoda blokowej iteracji podprzestrzennej jest odpowiednia dla wszystkich typów macierzy mas (rozłożonej, skupionej z rotacjami, skupionej bez rotacji). Zakres stosowania tej metody jest ograniczony do trybu modalnego. Jeżeli wybrana zostanie metoda Lanczosa, dostępne są dwa pozostałe tryby: pseudomodalny i sejsmiczny.

Weryfikacja Sturma — opcja pozwalająca na ustalenie wartości własnych pominiętych podczas procesu weryfikacji.

Metoda blokowej iteracji podprzestrzennej polega na jednoczesnych iteracjach wektora w podprzestrzeni o ustalonym wymiarze. Każdy wektor, dla którego wykonany został proces zbieżności, jest usuwany z podprzestrzeni pracy, a w jego miejsce dodawany jest nowy wektor. Ortogonalność tych wektorów jest zapewniana na każdym kroku iteracyjnym. Stosowane jest następujące kryterium zbieżności:

( 2 )

gdzie:

i, k — odpowiednio numer postaci i numer kroku iteracyjnego

tol — tolerancja, która jest definiowana w polu edycyjnym Tolerancja.

Wyniki analizy modalnej i wyboczeniowej są wyznaczane z określoną dokładnością, według następującego wzoru:

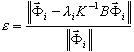( 3 )

Gdy proces zbieżności przebiega wolno, zaleca się zastosowanie procedury przesunięć w analizie modalnej:

( 4 )

gdzie:

K_σ = K — σ M,

σ — wartość przesunięcia.

Jeżeli włączona jest opcja Przesunięcia aktywne, procedura zostanie włączona; parametrem tej procedury jest liczba iteracji pomiędzy dwoma następnymi przesunięciami.

Uwaga: Należy unikać ustawienie zbyt małej liczby iteracji między kolejnymi przesunięciami. Powoduje to częste skupiska zbrojenia i rozkład przesuniętej macierzy sztywności K_σ. Są to czasochłonne operacje w szczególności dla dużych zadań.

Procedura przesunięć nie powinna być stosowana do analizy zadań wyboczeniowych, gdyż istnieje niebezpieczeństwo przesunięć widm wartości własnych w kierunku ujemnego obciążenia krytycznego (a co za tym idzie pominięcia dodatnich obciążeń krytycznych), jeżeli oczywiście występują dla konstrukcji ujemne wartości własne.

Określone pary własne są sortowane w następujący sposób | λ1 |≤ | λ 2 |≤ ... ≤ | λ n |, co powoduje umiejscowienie minimalnych parametrów obciążenia krytycznego w górnej części tabeli z wynikami.

Patrz również:

Blokowa iteracja podprzestrzenna — wykorzystanie przesunięcia