使用成分平均应力状态独立识别损坏萌生。

在基于能量的材料降解方案中，Helius PFA 使用成分平均应力状态独立识别基体和纤维成分中的损坏萌生。基体和纤维损坏萌生准则与此前所述的成分失效准则（基体成分失效准则和纤维成分失效准则）相同。当基体或纤维成分内发生损坏萌生后，相应的标量损坏变量（对于基体，为 D m；对于纤维，为 D f）开始从零演变到 Unity。损坏变量（D m 和 D f）充当如下所示的各复合模量的刚度缩减系数。

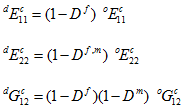
在上方损坏的复合模量的表达式中，前上标 d 表示量为降低（或损坏）量，而前上标 o 表示量为原始（未损坏）量。在上述方程中，如果 Dm > 0，则 Df,m 理解为表示 Dm；否则，Df,m 理解为表示 Df。

请注意，损坏的剪切模量如何依赖于 Dm 和 Df。如果两个成分均失效，将强制剪切模量以非线性方式降低。这将强制执行严格递减函数以进行降低，从而确保耗散的能量始终为正值。

当一个或两个成分材料发生损坏萌生后，我们必须拥有成分损坏演变的表达式，其适用于材料可能展现出的任何应变状态。为实现此目的，可以利用适合每种成分（纤维和基体）的应力和应变的有效标量测量。为了预测基体成分内的损坏演变，我们定义了有效应力和应变，如下所示。

基体的有效应力：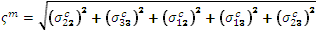

基体的有效应变：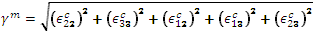

为了预测纤维成分内的损坏演变，我们定义了有效应力和应变，如下所示。

纤维的有效应力：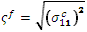

纤维的有效应变：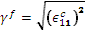

应当强调的是，这些有效基体和纤维值直接从复合材料平均应力和应变分量计算，而无需借助 MCT 分解。

成分损坏变量的演变以如下所示的这些有效应变来表示。

Df 是纤维损坏变量 (0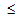Df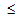1)，计算方式如下

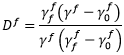
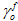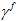其中， 是 在损坏萌生时的值，而 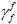是在材料完全降解（达到零刚度）时 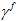的值。

Dm 是基体损坏变量 (0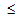Dm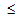1)，计算方式如下

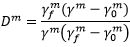
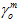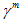其中， 是 在损坏萌生时的值，而 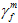是在材料完全降解（达到零刚度）时 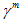的值。

应再次强调的是，已完全降解材料的耗散能量与 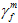和 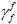成直接正比关系。因此，通过使 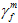和 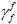与单元大小成正比来减轻网格敏感度，由以下等式得出

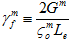
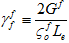
其中，Gm 和 Gf 是基体和纤维成分达到完全降解条件时耗散的复合能量密度。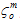 和 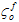是基体和纤维在损坏萌生时各自的有效应力，Le 是有效单元长度。

离散区间划分

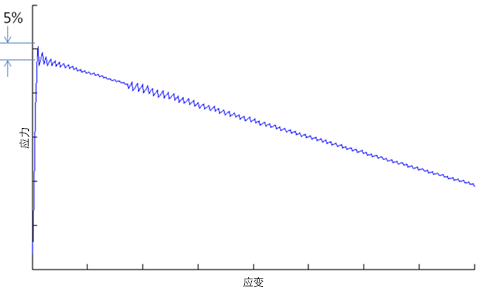
当线性降解复合材料时（如下所示），Helius PFA 基于能量的损坏功能将使用多个离散区间。每个区间将使用割线模量按该特定区间来定义复合材料的响应。对于总能量表示的图形类似于等腰三角形的问题，区间将精确捕获复合材料的响应。

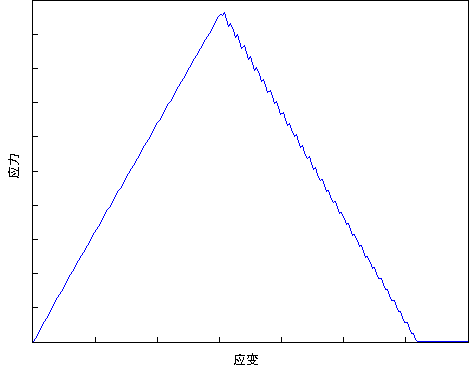
对于总能量表示严重扭曲三角形的分析（如下所示），区间划分将不再于早期应变级别准确地捕获复合材料的线性软化。这完全取决于用于实现问题最快速且最可靠的收敛性的区间数。具体而言，临近失效的应变级别下的应力割线区间将保留较高的刚度，并且可能导致对复合材料应力状态的失实描述。如果在您的分析中定义的线性降解曲线所具有的最终有效应变超过原始有效应变的 100 倍，请联系 Autodesk 以获取支持。