Explicit-Dynamikalgorithmen sind bei sehr nichtlinearen Simulationen äußerst robust, insbesondere für Kontaktprobleme mit großen Verformungen, die große Gleitbewegungen und Reibung umfassen. Ebenso bei extrem nichtlinearem Materialverhalten, wie z. B. bei großen plastischen Verformungen. Derartige Simulationen sind in einem impliziten Solver, der nichtlineare Gleichungen mit der Newton-Methode löst, sehr schwierig zu erzielen.
Bisher wurden Explicit-Codes verwendet, um sich an die quasi-statische nichtlineare Lösung heranzutasten, indem zur Minimierung der dynamischen Effekte eine ausreichend lange Dauer für die Last gewählt und so eine annähernd quasi-statische Lösung erzielt wurde. Dieses Konzept einer näherungsweisen statischen Lösung kann man quantifizieren, indem man den in allen Simulationen auftretenden Energieausgleich berücksichtigt. Für jedes Finite-Element-Modell kann der Energieausgleich wie folgt ausgedrückt werden:
KE + IE + VD = WE
Dabei ist KE die kinetische Energie, IE die interne Energie(Dehnungsenergie), VD die viskose Dissipation (Dämpfung) und WE die externe Arbeit, die durch die angewendeten Lasten im Modell durchgeführt wird. Bei herkömmlichen quasi-statischen Formulierungen wird davon ausgegangen, dass die Geschwindigkeiten null sind, und der Energieausgleich wird zu:
IE = WE
Einfach ausgedrückt: Interne Energie ist gleich externer Arbeit. Um eine annähernd quasi-statische Lösung im Explicit-Dynamikalgorithmus zu erhalten, soll die Größe der kinetischen Energie und der viskosen Dissipation in der Lösung im Vergleich zur Größe der internen Energie und der externen Arbeit verringert werden. Zu diesem Zweck wird die Dauer des Ereignisses so lang gewählt, dass die kinetische Energie ein kleiner Bruchteil der internen Energie ist. Dies ist in gewisser Weise subjektiv, und die Dauer wird mittels Versuch und Irrtum so gewählt, dass die kinetische Energie bei 1 bis 2 Prozent der internen Energie liegt. Erstaunlicherweise können quasi-statische Lösungen in sehr kurzer Zeit erreicht werden – viel schneller als man dies bei einer statischen Lösung normalerweise erwarten würde. In der Regel liegt die Dauer letztendlich im Millisekundenbereich.
Mit dem automatischen quasi-statischen Verfahren muss der Benutzer nicht mehr mit Versuch und Irrtum arbeiten, sondern kann stattdessen einen automatischen Multitest-Algorithmus einsetzen. Das Ziel ist, dass die freie kinetische Energie weniger als 1 % der internen Energie beträgt. Die freie kinetische Energie wird definiert als die kinetische Energie an allen Rasterpunkten im Modell, die keine vorgegebenen Verschiebungsrandbedingungen aufweisen. Man wählt eine anfängliche Dauer, die in der Regel ca. tausend Zeitschritte beträgt. Bei Anwendung der Last der Verschiebungssteuerung wird überprüft, dass die Geschwindigkeit, mit der die Knoten vorgegeben werden, nicht mehr als 5 % der minimalen Wellengeschwindigkeit eines der Materialien im Modell beträgt. Wenn dies der Fall ist, wird eine Dauer mit mehr als 1000 Zeitschritten gewählt, damit die Bewegung bei 5 % der Wellengeschwindigkeit stattfindet. Daher gibt es anfangs möglicherweise einige Versuche, die deutlich mehr Zeitschritte benötigen. Der erste Versuch ist jedoch wirklich nur ein Versuch, ein Schätzwert für die Dauer als Berechnungsgrundlage für einen anfänglichen Energieausgleich. Abbildung 1 zeigt eine Verlaufsdarstellung eines typischen Energieausgleichs, der möglicherweise beim ersten Versuch erzielt wird.
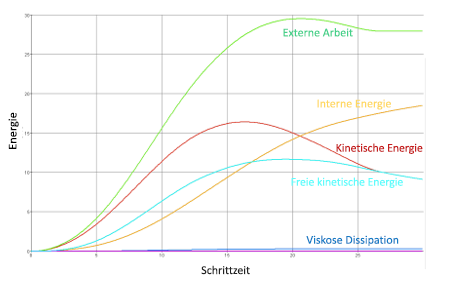
Abbildung 1: Typische Darstellung des Energieausgleichsverlaufs für den ersten Versuch
Nach dem ersten Versuch wird ein proprietärer Algorithmus angewendet, der den Energieausgleich über die gesamte Dauer des ersten Versuchs betrachtet und die interne Energie mit der kinetischen Energie vergleicht. Anhand dieses Algorithmus wird ein geeigneter Multiplikator für die Versuchsdauer berechnet, um die Simulation zu wiederholen. Dieser Multiplikator ist immer größer als 1,0 und liegt in der Regel im Bereich zwischen 5 und 20. Die Versuchslösung wird verworfen, und der zweite Versuch wird mit der neuen, längeren Dauer ausgeführt.
Abbildung 2 zeigt eine typische Darstellung des Energieausgleichsverlaufs für den zweiten Versuch. Die freie kinetische Energie wird im Vergleich zum ersten Versuch minimiert. Auch hier wird der proprietäre Algorithmus genutzt, um den neuen Energieausgleich bei diesem Versuch zu analysieren und so einen Multiplikator zu berechnen.
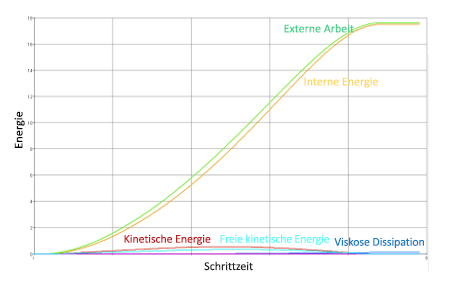
Abbildung 2: Typische Darstellung des Energieausgleichsverlaufs für den zweiten Versuch
Der Vorgang ist abgeschlossen, wenn der Multiplikator kleiner als 1,0 ist – die näherungsweise quasi-statische Lösung ist erreicht. Wenn nicht, wird eine neue Dauer aus dem Multiplikator mal der vorherigen Dauer berechnet. Der Vorgang wird wiederholt, indem Versuch Nummer 2 verworfen und Versuch Nummer 3 durchgeführt wird. Der Algorithmus unternimmt bis zu vier Versuche. Wenn nicht innerhalb von 4 Versuchen eine Konvergenz erreicht wird, ist wahrscheinlich keine quasi-statische Lösung möglich. Die meisten Modelle konvergieren innerhalb von zwei Versuchen. Einige brauchen drei Versuche. Vier Versuche sind selten. Die Modelle, die bei vier Versuchen nicht konvergieren, knicken in der Regel während der großen Verformungsbewegung. Im Grunde sind sie instabil.
In einer quasi-statischen Analyse ist das Konzept der Zeit dimensionslos. Die Zeit ist einfach eine Pseudozeit, die die Anwendung der transienten Lasten und/oder vorgeschriebenen Randbedingungen misst. Die ermittelte Lösung zeigt die Entwicklung der nichtlinearen Lösung durch den Prozess der Anwendung der Lasten innerhalb dieses Pseudozeitrahmens. Das quasi-statische Verfahren findet die kleinstmögliche Dauer, die mit dem oben beschriebenen iterativen Prozess die näherungsweise quasi-statische Last erzeugt.
Der Benutzer gibt eine Dauer für die Simulation an und stellt Amplitudenkurven bereit, die die Randbedingungen für transiente Last und/oder Zwangsverschiebung im Zeitverlauf beschreiben. Die Dauer ist einfach eine Pseudozeit. Sie kann zwischen 0 und 1, zwischen 0 und 1 Millisekunde oder zwischen 0 und 1000 liegen.
Die Dauer der Simulation und die Dauer der Amplitudenkurven müssen übereinstimmen. Die quasi-statische Prozedur wertet die Amplitudenfunktionen aus, während die Simulation ausgeführt wird. Dabei ist zu beachten, dass die vorgegebene Dauer in eine interne Dauer skaliert wird, die gerade lang genug ist, um die kinetische Energie in der Aufgabenstellung zu minimieren.
Es muss angegeben werden, wie viele Schritte in der Lösung ausgeführt werden sollen. Die vorgegebene Anzahl von Schritten ist 1, was für eine monotone Last angemessen ist. In der Regel würde man die Lasten und Randbedingungen mit einem linearen Anstieg von 0 bis 1 vorschreiben, wie in Abbildung 3 dargestellt.

Abbildung 3: Amplitude mit monotoner linearer Steigung
Die quasi-statische Prozedur wertet die Amplitude am Anfang und Ende der einzelnen Schritte aus und berechnet die Differenz (Δ) zwischen den jeweiligen Anfangs- und Endwerten. Dies ist das Belastungs- oder Verschiebungsinkrement, das während des Schritts angewendet wird. Die Last wird nicht mithilfe der Funktion für Amplitude mit linearer Steigung angewendet. Stattdessen wird automatisch eine "S-förmige" Amplitude in der in Abbildung 4 gezeigten Form erstellt, und der Wert Δ wird als Skalierungsfaktor verwendet.
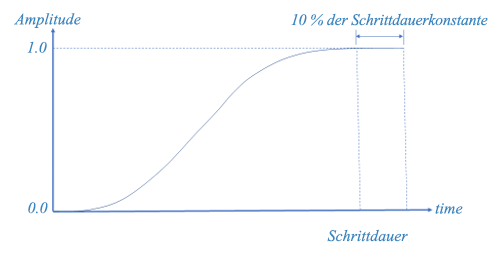
Abbildung 4: Interne Konstruktion der S-förmigen Amplitudenkurve
Wie abgebildet, weist die Amplitude sowohl am Anfang der Dauer als auch am Ende der Dauer eine Nullneigung auf. Die letzten 10 % der Dauer sind konstant. Die Länge der verwendeten internen Testdauer ist in diese interne Amplitudenkurve integriert. Die Form der S-Kurve wird so gewählt, dass dynamische Effekte minimiert werden. Angenommen, Randbedingungen sollen mit dem tatsächlichen linearen Anstieg, der wie üblich bei Null beginnt, vorgeschrieben werden. Dann wäre die Geschwindigkeit der vorgeschriebenen Randbedingungsknoten ein konstanter Wert, der zum Zeitpunkt Null einen Impuls auf das Modell aufsetzt. Die in Abbildung 4 dargestellte S-förmige Amplitude verringert dieses Problem. Bei nicht monotonen Lasten muss angegeben werden, dass die Simulation in mehreren Schritten ausgeführt werden soll. Betrachten wir den einfachen, nicht monotonen Be-/Entlastungsfall in Abbildung 5.
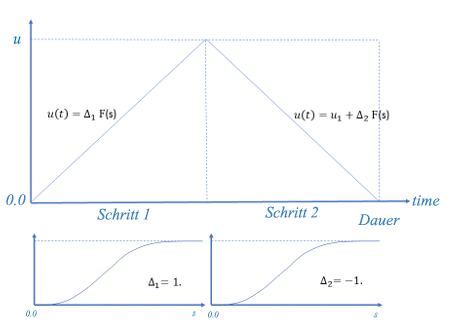
Abbildung 5: Nicht monotone Be-/Entlastungsamplitude, unterteilt in zwei Schritte
In diesem Fall soll das Modell bis zu einem vorgegebenen Wert belastet und dann wieder bis auf Null entlastet werden. Diese Simulation sollte zwei Schritte ausführen. Im ersten Schritt erfolgt eine Auswertung der vom Benutzer angegebenen Amplitude zum Zeitpunkt 0 sowie der Zeit, die der Hälfte der vom Benutzer angegebenen Dauer entspricht. Daraus wird die Amplitudenänderung berechnet: Δ1 = +1. Anschließend wird der quasi-statische Algorithmus ausgeführt, der die S-förmige interne Amplitudenfunktion zur Berechnung von quasi-statischer Reaktion einführt. Hierfür können bis zu vier Versuche erforderlich sein, wie oben beschrieben. Sobald der erste Schritt abgeschlossen ist, wird die Änderung der Verschiebung vom Ende des ersten Versuchs bis zum Ende des zweiten Versuchs berechnet: Δ2 = -1.
Die inkrementellen Verschiebungen im zweiten Schritt werden zu den Gesamtverschiebungen (vom ersten Schritt aus) hinzugefügt, um die Gesamtverschiebungen zu erhalten. Zu beachten ist, dass bei Lösungen mit mehreren Schritten alle Schritte mit Ausnahme des ersten beim ersten Versuch eine Versuchsdauer verwenden, die der endgültigen Dauer des vorherigen Versuchs entspricht. Der Grund ist, dass beim vorherigen Versuch bereits eine geeignete Dauer gefunden wurde, die näherungsweise quasi-statischen Ergebnisse liefert.
Die Auswahl der für eine Simulation zu verwendenden Anzahl an Schritten wirkt sich deutlich auf die Berechnungszeit aus, die zum Abschließen der Simulation benötigt wird. Jeder Schritt durchläuft den Versuchsalgorithmus, um eine quasi-statische Lösung zu suchen. Im Allgemeinen ist die Berechnungszeit für die Berechnung von Schritt 1 ungefähr genauso lang wie für die Berechnung von Schritt 2. Bei dem in Abbildung 5 dargestellten Beispiel für Be-/Entlastung würde das Aufteilen der Simulation in vier Schritte nicht zu einer besseren Lösung beitragen; die Ausführung würde aber doppelt so lange dauern. Eine sorgfältige Beurteilung der Anzahl der zu verwendenden Schritte ist wichtig für die Genauigkeit der Lösung. Betrachten wir das vorherige Beispiel einer Be-/Entlastungsaufgabe mit dem in Abbildung 5 dargestellten linearen Anstieg bzw. Rückgang.
Wenn der Benutzer für diese Simulation drei Schritte auswählt, wie in Abbildung 6 dargestellt, wird die maximale Verschiebung vollständig ausgelassen. Im ersten Schritt wird die Benutzeramplitude am 1/3-Punkt der Dauer ausgewertet, um ein Verschiebungsinkrement von Δ1 = 0.667 zu erzielen.
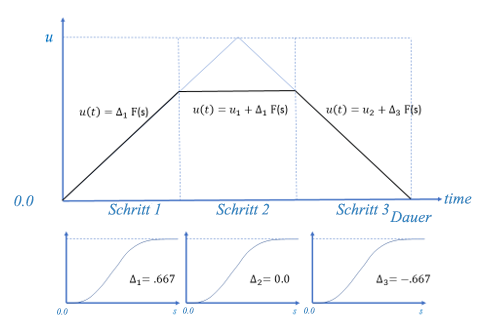
Abbildung 6: Nicht monotone Be-/Entlastungsamplitude, unterteilt in drei Schritte
Im zweiten Schritt wird die Benutzeramplitude am 2/3-Punkt der Dauer ausgewertet, um ein Verschiebungsinkrement von Δ2 = 0 zu erreichen. Dieser Schritt errechnet eindeutig nur eine Null-Reaktion und verpasst die maximale Verschiebung völlig. Im letzten Schritt würde die Dauer am Ende ausgewertet und ein Verschiebungsinkrement von Δ3 = -0.667 erreicht. Dadurch würde die Last entfernt. Es würde 50 % länger dauern, zu dieser Lösung zu kommen, und die maximale Verschiebung würde dabei verpasst werden.
Die Lösung, die wir in jedem Schritt erhalten, ist eine transiente Lösung in Pseudozeit. Da die Ergebnisse in der Regel sehr nichtlinear und pfadabhängig sind, werden Ergebnisse während der Pseudozeit jedes einzelnen Schritts an einer bestimmten Anzahl von Punkten angezeigt. Die vorgegebene Anzahl der Ergebnisse pro Schritt ist 10. Dieser Wert kann in eine größere oder kleinere Zahl geändert werden. Hinweis: Die Ergebnisse können recht umfangreich sein, und die Verwendung einer großen Anzahl von Ergebnissen pro Schritt kann zu sehr großen Dateien führen.