Die explizite Dynamikmethode eignet sich ideal für die Modellierung von äußerst nichtlinearen, verformungsreichen und kontaktgeprägten Aufgabenstellungen, bei denen Auswirkungen, Mehrkörperkontakte und sehr nichtlineares Materialverhalten eine Rolle spielt.
Im Allgemeinen ist das Durchführen von nichtlinearen expliziten Simulationen oft einfacher als das Durchführen von linearen Simulationen. Der Benutzer muss keine „Konvergenzeinstellungen“ anpassen, wie es für lineare Solver erforderlich ist, und startet die Simulation einfach ohne Berücksichtigung der Linearität des Systems.
Das Verfahren der expliziten Dynamik eignet sich besonders für die Simulation sehr großer Modelle, egal wie nichtlinear das Problem sein mag. Der Hauptvorteil ist, dass es kein zusammengesetztes System algebraischer Gleichungen gibt, das für jeden Zeitschritt gelöst werden muss, wie dies bei herkömmlichen impliziten Finite-Element-Formulierungen der Fall ist.
Ein expliziter Solver bildet einfach die dynamischen Gleichgewichtsgleichungen für das Finite-Element-Modell an den einzelnen Zeitinstanzen und verwendet eine explizite Integrationsregel, um zeitmäßig voranzuschreiten. Kurz gesagt: Da keine große Systeme algebraischer Gleichungen gelöst werden müssen, ist der Speicherbedarf gering und jeder Zeitschritt kann äußerst effizient berechnet werden. Wir werden sehen, dass der explizite Algorithmus einen relativ kleinen Zeitschritt erfordert. Daher ist es sehr wichtig, dass die Kosten der einzelnen Schritte niedrig sind.
Materiallöschung
Mit Autodesk Explicit können Kriterien zum Löschen von Materialien definiert werden, die Materialausfälle und somit die Entfernung aus der Simulation steuern. Dazu definiert man einfach einen Höchstwert für verschiedene Dehnungsmaße, die das Material nicht übersteigen darf. Wenn die benutzerdefinierten Kriterien an einer finiten Position im Modell erfüllt sind, entfernt Autodesk Explicit das Material an dieser Position und löscht das entsprechende Element aus dem Netz. Typische Dehnungsmaße zum Löschen sind die äquivalente plastische Dehnung und die maximale Hauptdehnung.
Wenn die Materiallöschung in einer Simulation verwendet wird, berücksichtigt Autodesk Explicit die Erosion der finiten Elemente durch kontinuierliche Aktualisierung der Kontaktflächen, um neu freigelegte Bereiche des Modells zu betrachten. Durch die Materiallöschung in Verbindung mit der Oberflächenerosion kann man das Modell auseinander ziehen und durchlöchern.
Starre Körper
Mit einer einzigen Deklaration kann festgelegt werden, dass ein Teil des Modells starr ist. Autodesk Explicit berechnet dann automatisch den Schwerpunkt und alle Eigenschaften des starren Körpers für das Bauteil (z. B. Massenträgheitsmomente und Gesamtmasse) sowie die Reaktion des Bauteils mithilfe von Gleichungen für die Dynamik von starren Körpern. Da das Bauteil starr ist, verformt es sich nicht lokal, sodass es im Bauteil keine Spannung oder Dehnung gibt. Kontaktbedingungen zwischen Bauteilen werden automatisch beibehalten, unabhängig davon, ob ein Bauteil starr ist oder nicht. Das Beste daran ist, dass starre Bauteile nicht an der Bestimmung des stabilen Zeitschritts beteiligt sind.
Kontakt
Die Kontaktmodellierung ist innerhalb der Technik der expliziten Dynamik sehr einfach. Man definiert einfach alle Bauteile, aus denen das zusammengebaute Modell besteht. Die Anwendung überwacht automatisch die Kollisionen zwischen den Bauteilen und erzwingt eine kinematische Einhaltung. Die Anzahl der Bauteile, die einander berühren können, ist nicht begrenzt. Der Aufwand für den Benutzer ist äußerst gering.
Der Benutzer gibt höchstens das Reibungsverhalten zwischen den verschiedenen Bauteilen an (der vorgabemäßige Reibungskoeffizient ist Null) oder legt fest, dass die Kontaktflächen miteinander verschweißt werden (Vorgabe ist ein nicht verschweißtes/trennbares Flächenpaar). Autodesk Explicit überwacht und verfolgt ständig die Nähe der verschiedenen freien Flächen des Modells, obwohl alle großen Verformungen und Drehungen zur Erzwingung der kinematischen Konformität bei Kollisionen erkannt werden.
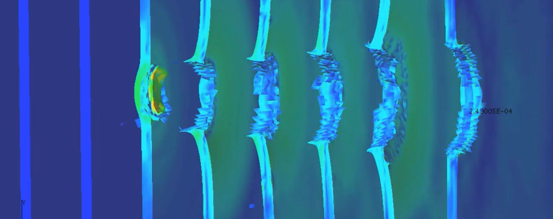
Eine der vielseitigsten Funktionen des Kontakterkennungs-Algorithmus besteht darin, dass die Flächen des Modells bei Materialerosion automatisch neu aufgebaut werden und neue Flächen aufgrund der Elementlöschung freigelegt werden. Abbildung 2 zeigt die Simulation eines Vogelschlags bei einer Turbine.
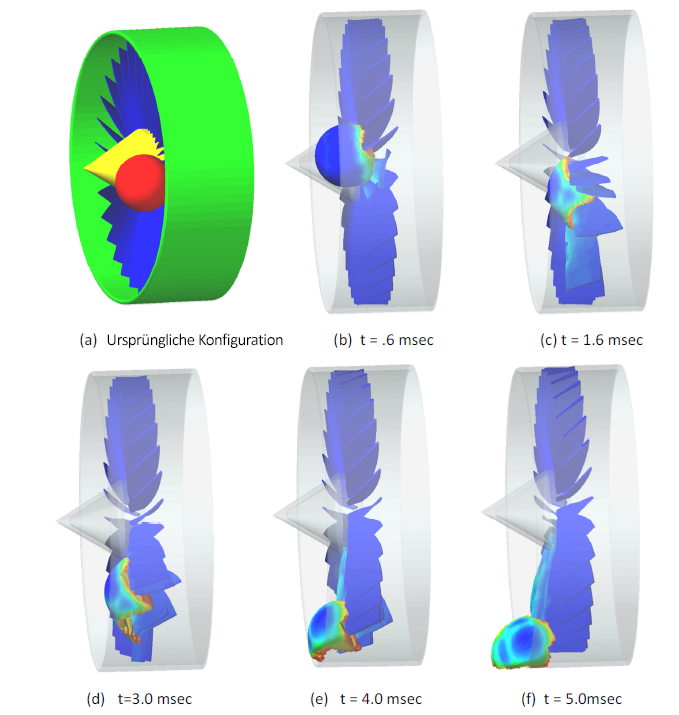
Abbildung 2: Beispiel für automatische Kontaktverfolgung
Der „Vogel“ wird als Kugel modelliert, die aus einem weichen Kunststoffmaterial besteht und mit 300 mph in die Turbine einschlägt. Die Turbinenschaufeln sind aus Stahl, und die Turbine dreht sich mit 6000 U/min. Der automatische Kontakt überwacht Kollisionen zwischen der Kugel und den Schaufeln sowie zwischen den einzelnen Schaufeln. Die Kugel und die Schaufeln werden ebenfalls auf Kontakt mit dem Außenmantel überwacht. Der kugelförmige Vogel hat Kriterien zur Materiallöschung auf der Grundlage plastischer Dehnung mit einem Wert von 30 %. Bei den Stahlturbinenschaufeln haben die Kriterien zur Materiallöschung auf der Grundlage plastischer Dehnung einen Wert von 100 %.
Beim Auftreffen der Kugel auf die Flügel kommt es zu einer starken Verformung der Kugel und zu Materialerosion. Bei jedem Zeitschritt während der Simulation werden alle Kontaktflächen automatisch neu erstellt. Dabei ist zu beachten, dass die Vorderkante der Schaufeln ebenfalls der Erosion ausgesetzt ist, sodass Autodesk Explicit zwei erodierende Teile, die sich aktuell berühren, gleichzeitig neu erstellt. Die Kollisionserkennung und die Neuerstellung von DGMs erfolgen automatisch und erfordern keine Benutzereingriffe.
Explizite Integration
Der Schlüssel zur Vielseitigkeit des expliziten Dynamikverfahrens ist der Integrationsalgorithmus, nach dem es benannt ist. Bei Zeit t berechnet der Finite-Elemente-Solver alle auf das Netz wirkenden Kräfte, sowohl interne Kräfte (aufgrund der Spannungen in den Elementen) als auch externe Kräfte (aufgrund der angewendeten Lasten).
Beschleunigung(t) = [Externe Kräfte(t) - Interne Kräfte(t)]/KnotenmasseDas Geheimrezept, das explizite Dynamik so effizient macht, ist die Verwendung einer konzentrierten Knotenmasse. Das bedeutet, dass wir alle Knotenbeschleunigungen berechnen können, ohne auf einen linearen algebraischen Solver zurückgreifen zu müssen. Sobald die Beschleunigungen zum Zeitpunkt t bekannt sind, werden die Knotenwerte der Beschleunigungen explizit in die Zeit integriert, um die Knotenwerte der Geschwindigkeiten und Verschiebungen zum Zeitpunkt t+Δt zu erhalten:
Geschwindigkeit(t + Δt) = Geschwindigkeit(t) + Δt ・ Beschleunigung(t)
Verschiebung(t + Δt) = Verschiebung(t) + ½Δt ・[Geschwindigkeit(t) + Geschwindigkeit(t + Δt)]
Es könnte kaum einfacher sein. Der tatsächliche Rechenaufwand fällt im Schritt zur Berechnung der internen und externen Knotenkräfte an, wo die gesamte Finite-Elemente-Methode abläuft. Aber auch hier wird nur ein Bruchteil der Finite-Elemente-Berechnungen durchgeführt, die man bei herkömmlichen impliziten Finite-Element-Solvern findet. Beim expliziten Verfahren wird nur die rechte Seite der Bewegungsgleichungen gebildet.
Bei einem impliziten Solver dagegen bildet man die rechte Seite genauso, aber zusätzlich muss die globale Steifigkeitsmatrix zusammengefügt und das Gleichungssystem direkt gelöst werden. Bei nichtlinearen Modellen muss ein impliziter Solver die globale Systemmatrix bei jedem Zeitschritt neu bilden, neu zusammensetzen und neu gewichten. Hier zeigt sich deutlich, warum explizite Dynamik-Solver bei nichtlinearen Simulationen so effizient sind. Jeder explizite Zeitschritt ist buchstäblich um ein Vielfaches schneller als ein impliziter Zeitschritt.
Berechnungszeit für die Bildung der Elementkräfte benötigt wird, ist die tatsächliche Laufzeit für Ihre Simulationen direkt proportional zur Anzahl der Elemente im Modell. Wenn dann das Modell in jeder Richtung mit dem Faktor 2 verfeinert wird, sodass die Lösung achtmal so viele Elemente umfasst, würde man erwarten, dass die Lösung achtmal länger dauert. Tatsächlich würde es jedoch 16 Mal länger dauern, da die Zeitschrittgröße halb so groß ist wie das unverfeinerte Modell.
Automatische Zeitschrittsteuerung durch Stabilitätsgrenzen
Wenn sich etwas zu gut anhört, um wahr zu sein, steckt meistens mehr dahinter. In diesem Fall wird die oben beschriebene explizite Integrationsmethode durch einen Stabilitätsgrenzwert bestimmt. Einfach ausgedrückt: Es gibt eine kritische Zeitschrittgröße, die beim expliziten Integrieren nicht überschritten werden darf. Diese sogenannte Stabilitätsgrenze hängt von der Netzgröße und den Materialeigenschaften ab.
Bei einer dynamischen Simulation mit einem herkömmlichen impliziten Solver gibt man in der Regel die Dauer der zu berechnenden Antwort und die Anzahl der zu verwendenden Zeitschritte an. Wenn man beispielsweise eine Simulationsdauer von einer Sekunde bei 100 Zeitschritten haben möchte, beträgt die Zeitschrittgröße 0,01 Sekunden und bleibt während der Analyse fest. Bei einer expliziten Dynamiksimulation kann man dagegen nur die Gesamtdauer angeben. Der explizite Dynamik-Solver wählt die Zeitschrittgröße automatisch so aus, dass sie unterhalb der Stabilitätsgrenze des Modells bleibt. Der Nutzer hat keine Kontrolle über die Anzahl der Zeitschritte, die der explizite Solver benötigt.
Wie wird also die Stabilitätsgrenze bestimmt? Die genaue Bestimmung der Stabilitätsgrenzen eines Modells erfordert sehr viel hoch komplizierte Mathematik. Die technisch korrekte Antwort lautet, dass sie von der höchsten Eigenfrequenz im Modell abhängt. Man kann es aber auch ganz einfach anhand der Elementgröße und der Wellengeschwindigkeit in den Materialien betrachten. Die kritischen Zeitschritte für die einzelnen Element können berechnet werden als die Zeit, die zum Übertragen einer Welle über die Länge des jeweiligen Elements (d. h. Elementlänge/Wellengeschwindigkeit) benötigt wird. Der kritische Zeitschritt für die Simulation ist einfach der kleinste Wert für alle Elemente des Netzes.
Die Wellengeschwindigkeit wird berechnet als Quadratwurzel aus dem Verhältnis des Materialmoduls und der Materialdichte. Es gibt verschiedene Wellengeschwindigkeiten (z. B. Längs-, Scher-, Dilatationsgeschwindigkeit usw.). Zur Veranschaulichung dieses Konzepts wird die Längswellengeschwindigkeit basierend auf dem Elastizitätsmodul verwendet (die genaue mathematische Form in Autodesk Explicit ist die dilatationsbezogene Wellengeschwindigkeit). Bei einem Stahlmaterialmodell mit einem Elastizitätsmodul von 200 GPa und einer Dichte von 7800 N/m3 beträgt die Wellengeschwindigkeit etwa 5000 m/s. Eine wirklich sehr große Zahl Jedem Element im Netz ist eine charakteristische Länge zugeordnet. Hier spielt Genauigkeit keine besonders große Rolle. Nehmen wir einfach an, dass die charakteristische Elementlänge die kürzeste Kante des Elements ist. Wenn es im Stahlbauteil also Elemente mit einer Größe von 1 mm gibt, ist der Zeitschritt in der expliziten Dynamik etwa 2 ・10-7 s.
Ja, der Zeitschritt ist kleiner als eine Mikrosekunde. Dies ist bei expliziter Dynamik recht häufig der Fall. Es sind viele Zeitschritte auszuführen. Aber jeder Zeitschritt wird sehr effizient ausgeführt, sodass die Gesamtlaufzeit ebenfalls effizient ist.
Abbildung 3 zeigt eine Skizze einer Dilatationswelle, die sich über ein ungleichmäßiges Netz ausbreitet.

Abbildung 3: Übertragung einer Dilatationswelle in einem Netz
Jedes Element weist eine charakteristische Länge auf, die in der Abbildung allgemein als x0007 dargestellt wird. Jedes Element im Netz kennt seinen aktuellen Wert für die Dilatationswellengeschwindigkeit im Material an diesem Punkt (die Materialwellengeschwindigkeit kann sich in nichtlinearen Materialmodellen tatsächlich ändern). Es spielt keine Rolle, wo sich die Welle zu einem bestimmten Zeitpunkt befindet. Tatsächlich laufen viele Wellen durch das Netz. Das explizite Verfahren berechnet einfach die Übergangszeit über jedes Element und nimmt einen Zeitschritt, der dem Mindestwert im gesamten Modell entspricht.
Das Wichtigste dabei ist, dass der Nutzer sich um all dies nicht kümmern muss. Autodesk Explicit überwacht ständig die Stabilitätsgrenzen des Modells und wählt den Zeitschritt aus, während die Simulation fortschreitet.
Die wichtigsten Punkte, die man bei der stabilen Zeitschrittgröße bedenken sollte, sind folgende:
- Der stabile Zeitschritt ist direkt proportional zu den Elementgrößen. Durch Verfeinern des Netzes um den Faktor 2 wird der Zeitschritt um den Faktor 2 reduziert.
- Die Laufzeit des Modells ist direkt proportional zur Anzahl der Elemente im Modell und zur Anzahl der Zeitschritte, die zur Integration der Antwort über die Zeitdauer nötig sind. Durch Verfeinern des Netzes um den Faktor 2 in jeder Richtung wird die Anzahl der Elemente um den Faktor 8 erhöht, die Laufzeit wird jedoch 16 Mal länger.
- Der stabile Zeitschritt ist direkt proportional zur Quadratwurzel aus dem Materialmodul. Sehr harte Materialien wie Stahl haben einen kleineren stabilen Zeitschritt als weiche Materialien wie Gummi.
- Der stabile Zeitschritt ist umgekehrt proportional zur Quadratwurzel aus der Materialdichte. Schwerere Materialien haben einen größeren stabilen Zeitschritt, da es länger dauert, bis eine Welle sich über ein Material mit größerer Masse hinweg fortsetzt.