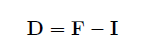The governing stress equilibrium equation is
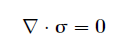 where σ is the stress. The mechanical constitutive law is
where σ is the stress. The mechanical constitutive law is
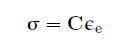 where C is the fourth order material stiffness tensor and εe is elastic strain.
where C is the fourth order material stiffness tensor and εe is elastic strain.
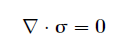
Equation 9
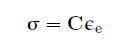
Equation 10
Small deformation theory
For small deformations, the total strain can be calculated as
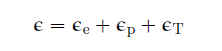 where ε, εp, and εTare the total strain, plastic strain, and thermal strain, respectively.
where ε, εp, and εTare the total strain, plastic strain, and thermal strain, respectively.
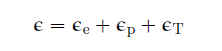
Equation 11
The thermal strain is computed as
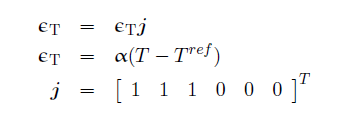 where α is the thermal expansion coefficient and Tref is reference temperature.
where α is the thermal expansion coefficient and Tref is reference temperature.
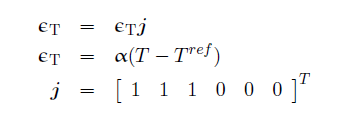
Equations 12 through 14
The plastic strain is computed by enforcing the von Mises yield criterion and the Prandtl-Reuss flow rule:


Equations 15 through 17
where f is the yield function, σm is Mises' stress, σy yield stress, εq is the equivalent plastic strain, andα is the flow vector.
Large deformation theory
The governing mechanical stressσ equilibrium equation, when the current spacial location of the part x in a deformed state may vary significantly from the undeformed reference configuration X state, (see Reference 3) is written as
 where the first Piola-Kirchoff stress tensor P is defined as
where the first Piola-Kirchoff stress tensor P is defined as
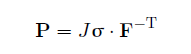 where σ is the stress tensor and
J is the determinant of the deformation gradient F, which is defined as
where σ is the stress tensor and
J is the determinant of the deformation gradient F, which is defined as
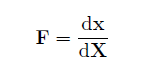

Equation 18
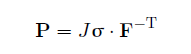
Equation 19
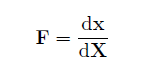
Equation 20
The Green Strain E is calculated as
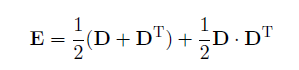 where the displacement gradient D is defined as
where the displacement gradient D is defined as
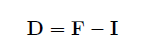 where I is the identity matrix. For small deformations, the total Lagrangian formulation will simplify and equate to the small deformation formulation.
where I is the identity matrix. For small deformations, the total Lagrangian formulation will simplify and equate to the small deformation formulation.
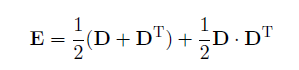
Equation 21