Papier blanc : Angle plan résolution de la solution CI IH

La condition fondamentale requise pour la solution IH est que la solution soit indépendante de l'historique : la solution doit être basée sur le but et les autres paramètres d'incidence uniquement à leurs états actuels.

Degré de liberté de l'angle plan résolution

Lorsque le but de position est donné pour une chaîne unique, un degré de liberté évident demeure : la rotation autour de l'axe Effecteur extrémité (axe EE). L'angle plan résolution permet de décrire ce degré de liberté de manière quantitative.

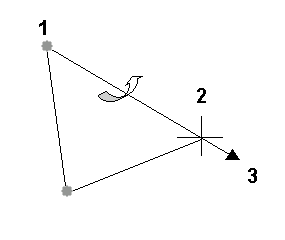
1. Connexion de départ

2. Effecteur extrémité

3. Axe EE

Plan de la solution

Le plan qui transmet toutes les connexions est appelé Plan de la solution. Lorsque les connexions ne reposent pas sur un plan, il peut être défini comme étant le plan qui (A) transmet la connexion de départ et l'effecteur d'extrémité et (B) est le plus proche de la connexion restante, dans un certain sens.

L'angle plan résolution décrit le degré de liberté du plan de la solution et contraint uniquement la connexion de départ.

Mapping de plan zéro

Afin de décrire le plan de la solution en termes de quantité numérique, il est nécessaire de définir ce que signifie 0 (zéro). Etant donné la position de l'effecteur d'extrémité, où se trouve le plan zéro (de la solution)? Le mapping de plan zéro prend l'axe EE comme argument et produit la normale du plan zéro.

Le système CI permet à des plug-ins de solution individuels de définir leurs propres mappings de plan zéro. Si aucun mapping n'est défini, le système CI fournit un mapping par défaut.

L'argument du mapping de plan zéro est un vecteur unitaire donnant le sens de l'axe EE. De même, le plan de la solution doit être fixe lorsque l'effecteur d'extrémité glisse le long de l'axe EE. Le mapping de plan zéro définit ainsi un champ de vecteur sur une sphère. Etant donné un point sur la sphère, il produit un vecteur unitaire tangentiel devant être interprété comme la normale du plan zéro.

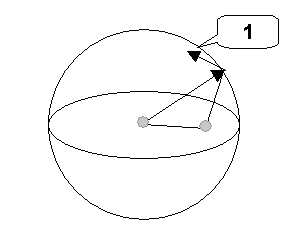
1. Normale du plan zéro

Basculement du plan de la solution

L'absence d'un champ de vecteur continu sur une sphère est un fait mathématique. Quoi que vous fassiez, il y aura toujours un point sur la sphère où les vecteurs avoisinants changent de manière prononcée. C'est au niveau de ce point que le plan de la solution bascule lorsque l'axe de l'effecteur d'extrémité s'en approche.

Cela est dû, d'une part, au fait que la condition indépendante d'historique nécessite l'affectation d'un vecteur fixe au point singulier. D'autre part, quel que soit le vecteur affecté, celui-ci sera très différent de certains autres vecteurs affectés à des points avoisinants.

Image de référence intrinsèque pour la sphère

Il est nécessaire de définir une image de référence pour la sphère afin de pouvoir définir le mapping de plan zéro. Cette image de référence est intrinsèque à la chaîne de connexion.

Une sphère peut être définie par le centre, le plan horizontal et le méridien (longitude zéro). Le centre est affecté à la connexion de départ.

La pose au moment où tous les angles de connexion se transforment en angles préférés est particulièrement importante. Appelons-la la pose préférée.

Le plan de la solution à la pose préférée est utilisé en tant que plan horizontal. L'angle plan résolution étant utilisé pour contrôler la connexion de départ, les angles préférés au niveau de la connexion de départ ne sont pas totalement intrinsèques. Il est également raisonnable de définir le plan horizontal avec le plan de la solution dérivé en affectant des zéros à la connexion de départ et des angles préférés aux autres connexions.

L'axe EE définit le méridien. La sphère est maintenant définie tel qu'illustré dans la figure suivante :

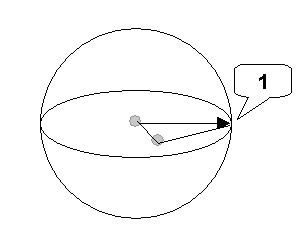
1. Axe EE

Toutes les connexions prennent des angles préférés. Le mapping de plan zéro doit être défini sur cette sphère.

En fait, l'API permettant au plug-in de solution de définir son propre mapping de plan zéro prend l'axe EE et la normale du plan de la solution à la pose préférée :

virtual const IKSys::ZeroPlaneMap*

 GetZeroPlaneMap(const Point3& a0,
 const Point3& n0) const

où a0 et n0 représentent, respectivement, l'axe EE et le plan de la solution à la pose préférée. ZeroPlaneMap est une fonction permettant d'affecter une normale de plan à chaque point de la sphère.

Mapping de plan zéro par défaut

Lorsque aucun mapping de plan zéro n'est fourni par les plug-in de solution (la Solution IH est elle-même mise en oeuvre en tant que module d'extension), le système CI en fournit un par défaut. Ce mapping est défini par les règles suivantes :

• A : pour chaque point de l'équateur, intersection du plan horizontal et de la sphère, le vecteur de la normale est défini en tant que vecteur vertical, pointant dans la même direction que la normale du plan de la solution à la pose préférée.
• B : pour tout point sur la sphère autre que les pôles nord et sud, il existe un grand cercle qui traverse ce point et les pôles nord et sud. Ce cercle rejoint l'équateur à deux points. L'un de ces points est plus proche du point donné. Le vecteur de la normale au point donné est dérivé en déplaçant de manière tangentielle la normale au point le plus proche sur l'équateur le long du grand cercle jusqu'au point.
  

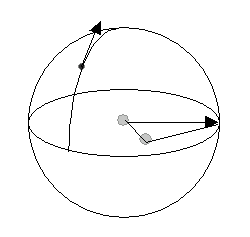
  Dérivation de la normale du plan zéro par défaut

Cette méthode ne s'applique évidemment pas aux pôles nord et sud. Ces derniers sont des points singuliers. Lorsque l'axe EE traverse les pôles, la normale change soudainement de direction et bascule à partir du point de vue de l'utilisateur.

La pose préférée est en général celle définie lors de l'affectation initiale de la solution. Ainsi, le plan sur lequel reposent les connexions correspond ici au plan horizontal. La règle A permet de garantir que la chaîne reste sur le plan lors du déplacement du but sur ce plan.

La règle B signifie que lorsque vous déplacez le but le long du grand cercle verticalement par rapport à l'équateur, la chaîne reste verticale, sauf si elle traverse les pôles, qui sont les points singuliers de ce mapping.

Espace parent

Jusqu'à présent, nous avons décrit les choses comme si l'univers entier était uniquement fait d'éléments CI. En réalité, la chaîne et le but CI peuvent se trouver à des points appartenant à des hiérarchies de transformation distinctes. Finalement, nous devons mapper vers un point de la sphère la position de l'effecteur d'extrémité décrite dans l'univers. La latitude et la longitude dépendent de l'emplacement de la sphère par rapport à la position de l'effecteur d'extrémité. L'espace de transformation parent dans lequel cette sphère va être placée est appelé Espace parent angle plan résolution – ou, si le contexte est clair, Espace parent.

L'espace parent ne peut varier pour ce qui est des paramètres CI. Deux choix sont actuellement disponibles :

• Connexion de départl'espace parent angle plan résolution est identique à l'espace parent de la connexion de départ.
• But CIl'espace parent angle plan résolution est l'espace parent du but CI.

Exemple 1

Si la connexion de départ et l'objectif sont directement originaires de l'univers, les deux types d'espaces parent donnent le même résultat. Dans l'exemple suivant, la connexion de départ est apparentée à l'objet A.

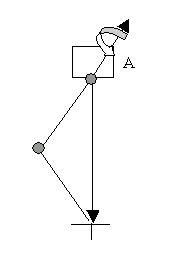
La chaîne CI est apparentée (via la connexion de départ) à l'objet A.

Supposons qu'il s'agisse de la pose définie lors de l'affectation de la solution CI. Il s'agit donc de la pose préférée. Le plan sur lequel reposent les connexions est le plan horizontal (mapping de plan zéro) de la sphère.

• A : l'espace parent est la connexion de départ. Dans ce cas, la sphère est apparentée à A. Lorsque A pivote autour de l'axe dessiné, la sphère pivote également. Le but est dans une hiérarchie de transformation distincte. Il ne bouge donc pas et l'effecteur d'extrémité y reste attaché en raison de la solution CI. Etant donné que la normale (de plan) est reliée à la sphère, elle pivote également avec A. La chaîne entière pivote donc avec l'objet parent.
• B : l'espace parent est le but CI. Supposons que l'objectif soit apparenté à l'univers. Dans ce cas, la sphère est apparentée à l'univers et reste donc fixe. La normale étant reliée à la sphère, la chaîne ne bouge donc pas lorsque A pivote.

Exemple 2

Dans l'exemple ci-dessous, une rotation existe dans l'espace parent lors de l'affectation de la solution CI.

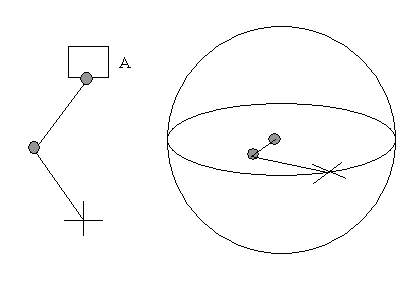
L'espace parent de la chaîne CI contient une rotation lorsque la solution CI est affectée.

Le parent A comporte une rotation de 90 degrés. Il s'agit d'un cas de figure où un utilisateur crée quatre structures sans solution CI, puis affecte ultérieurement une solution CI de la Structure02 vers la Structure04. Si nous apparentons la chaîne directement à l'univers, elle apparaît tel qu'illustré dans la figure de droite : le plan de la solution devient horizontal.

• A : l'espace parent est la connexion de départ. La sphère est reliée après la rotation de A et le " plan horizontal " coïncide donc avec le plan de la chaîne tel qu'affiché dans la fenêtre. Les points singuliers sont perpendiculaires à la connexion de départ en ce qui concerne le plan. Lorsque vous déplacez le but ou l'effecteur d'extrémité sur le plan, il n'atteint jamais les points singuliers et ne bascule pas.
• B : l'espace parent est le but CI. Supposons toujours que l'espace parent du but soit l'univers. Le " plan horizontal de la sphère devient horizontal, tel qu'illustré dans la figure de droite. Les points singuliers, les pôles, se trouvent sur le plan où reposent les connexions. Ainsi, lorsque vous déplacez le but ou l'effecteur d'extrémité de gauche à droite, ou inversement, l'effecteur d'extrémité traverse le point singulier et bascule.

Dans le cas de B, l'utilisateur ne voit jamais la figure de droite. Seule votre imagination vous permet de comprendre ce phénomène de basculement.

Exemple 3

Cet exemple décrit ce qui se produit lorsque la connexion de départ est ré-affectée. Supposons une chaîne CI contenant quatre noeuds de structure.

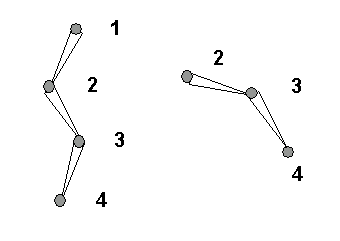
1. Structure01

2. Structure02

3. Structure03

4. Structure04

Les connexions de départ et de fin sont respectivement Structure01 et Structure04. Supposons que la pose illustrée dans la figure soit la pose préférée et que la Structure01 contienne une rotation. Si nous apparentons directement la Structure02 à l'univers, la hiérarchie de la Structure02 s'affiche, comme illustré dans la figure de droite.

Lorsque la connexion de départ est réaffectée à la Structure02, la sphère du mapping de plan zéro est alors basée sur la configuration de droite.

• A : l'espace parent est la connexion de départ. Dans ce cas, la sphère reliée à la configuration de droite sera apparentée à la Structure01. Elle sera identique à celle basée sur la Structure01 à la Structure04. La normale est donc la même et la chaîne reste stationnaire.
• B : l'espace parent est le but CI. Dans ce cas, la sphère demeure dans l'univers tandis que la Structure02 est apparenté à la Structure01. Lorsque la transformation de la Structure01 déplace la Structure04 à la position illustrée à gauche, l'observateur fixé à la sphère elle-même fixée à l'univers voit la Structure04 s'éloigner de la position neutre définie par la pose préférée. L'algorithme applique alors le mapping de plan zéro pour trouver la normale à la position déplacée. Celle-ci n'est généralement pas perpendiculaire à la fenêtre. Un basculement se produit donc une fois une nouvelle connexion de départ utilisée.

La chaîne ne bascule pas lorsque vous supprimez le but ou la solution et que vous en affectez un nouveau ou une nouvelle de la Structure02 à la Structure04. Pourquoi? L'affectation d'une connexion de départ n'a rien à voir avec la création d'une nouvelle chaîne ou d'un nouveau but CI. La connexion de départ est un des nombreux paramètres de CI. Sa réaffectation équivaut simplement à la modification de n'importe quel paramètre. Les autres paramètres restent inchangés. En particulier, l'angle plan résolution n'est pas touché par cette réaffectation.

La création d'une nouvelle chaîne ou d'un nouveau but CI est une toute autre chose. Il faut vous assurer que la chaîne de connexion reste fixe en définissant les paramètres appropriés. Vous définissez, en particulier, l'angle plan résolution sur une valeur permettant au plan de la solution de rester stationnaire dans la fenêtre.