Les sections ajourées sont obtenues à partir des sections laminées à chaud (sections en I laminées à chaud disponibles dans la base de sections) par découpage de l’âme suivant une ligne polygonale ou circulaire. Il existe deux types de section ajourée : à ouvertures hexagonales et à ouvertures circulaires.
Les barres ajourées ne sont dimensionnées que d’après la norme acier polonaise.
Pour la section ajourée, vous pouvez définir :
- Nom - attribue une caractéristique (nom) à la section. (Robot affecte automatiquement une caractéristique standard contenant le nom de la section sélectionnée dans la base de données et la figure x désignant la hauteur de la nouvelle section, p. ex. HP 8x36_8), où :
x = h + c pour les ouvertures hexagonales
x = h + c pour les ouvertures hexagonales avec plaquette intercalaire
x = H pour les ouvertures circulaires (H est la hauteur totale de la section définie par l’utilisateur)
- Couleur - indique la couleur de la section
- Spécifiez une section :
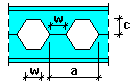
Ouvertures hexagonales :
c - profondeur de coupe
w - distance entre les ouvertures
a - espacement des ouvertures
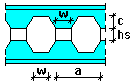
Ouvertures hexagonales avec plaquette intercalaire supplémentaire :
c - profondeur de coupe
w - distance entre les ouvertures
hs - hauteur de la plaquette intercalaire
a - espacement des ouvertures
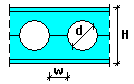
Ouvertures circulaires :
d - diamètre des ouvertures
w - distance entre les ouvertures
H - hauteur de la section
- Type de section - ce groupe d'options permet de sélectionner un type de section approprié.
- Angle gamma - permet d'indiquer l’angle gamma d'une section.
PROFILES A EVIDEMENTS HEXAGONAUX
Propriétés géométriques
Hauteur totale de la section : H = h + c + h s
Aire de la section transversale pour la section pleine
Ap = A + c * tw
Aire de la section transversale pour la section avec ouverture
Ao = A - c * tw
Aire de la section transversale en T de la membrure (section avec évidemment)
A = 0.5 * Ao
Aires des sections transversales efficaces au cisaillement
Ay = 2 * bf * tf – aire de la section transversale des ailes
Az = tw * (h - 2 * tf - c) – aire de la section transversale de l’âme dans la section la plus faible – avec ouverture
Position du centre de gravité de la section
vz = vpz = 0.5 * H
vy = vpy = 0.5 * bf
Moments d’inertie respectivement par rapports aux axes Y et Z de la section composée uniquement d'ailes :
- Pour la section pleine
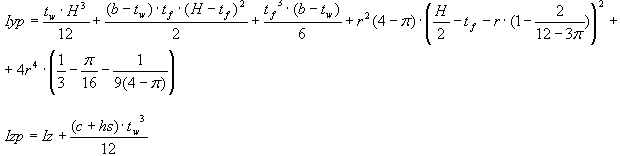
- Pour la section avec ouverture
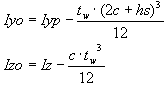
Moyenne arithmétique des moments d’inertie de la section affaiblie et non affaiblie :
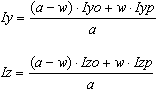
Moment d’inertie en torsion
PROFILES A EVIDEMENTS CIRCULAIRES
Propriétés géométriques
d - diamètre des ouvertures
w - distance entre les ouvertures
H - nouvelle hauteur de la section (hauteur totale de la section avec plaquette intercalaire)
Aire de la section transversale pour la section pleine
Ap = A + (H - h) * tw
Aire de la section transversale pour la section avec ouverture
Ao = A + (H - h - d) * tw
Aire de la section transversale en T de la membrure (section avec évidemment)
A = 0.5 * Ao
Aires des sections transversales efficaces au cisaillement
Ay = 2 * bf * tf – aire de la section transversale des ailes
Az = tw * (H - 2 * tf - d) – aire de la section transversale de l’âme dans la section la plus faible – avec ouverture
Position du centre de gravité de la section
vz = vpz = 0.5 * H
vy = vpy = 0.5 * bf
Moments d’inertie respectivement par rapport aux axes Y et Z de la section composée uniquement de membrures
Pour la section pleine
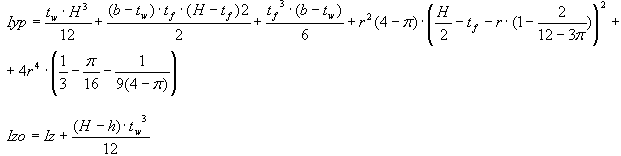
Pour la section avec ouverture
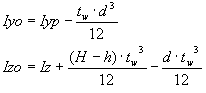
Moyenne arithmétique des moments d’inertie de la section affaiblie et non affaiblie :
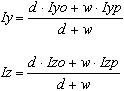
Moment d’inertie en torsion
Poids propre
PROFILES A EVIDEMENTS HEXAGONAUX
Étant donné que la section ajourée avec ouvertures hexagonales est faite à partir d'une section standard (dont les paramètres sont connus) sans presque aucune perte (excepté les extrémités de la section que l’on peut négliger), son poids est égal au poids de la section initiale.
G = g + Gs
g - Epaisseur de la section initiale
où :
h s *t w - Zone de section transversale d'une plaquette intercalaire
r s - Poids unitaire de l'acier
Par conséquent, le poids propre
PROFILES A EVIDEMENTS CIRCULAIRES
Le poids propre d'une section ajourée à ouvertures circulaires doit être calculé comme un poids de la section avec une plaquette intercalaire (hauteur 'H'), de la section transversale pleine, dont est déduit le poids des ouvertures.
Poids de la section initiale (à partir d'une base de données) : g
Epaisseur de la section pleine avec une plaquette intercalaire : g1 = g + rs * (H - h) * tw
Epaisseur de la section ajourée avec ouvertures circulaires
BASE DE DONNES DES SECTIONS AJOUREES
Des sections ajourées sont également disponibles dans la base de données de sections suivante :
- Base de données des sections polonaises - RPLNPro (sections à ouvertures hexagonales à partir des sections IPE - AIPE, IN - AIN et HEB - AHEB, à ouvertures hexagonales avec plaquettes intercalaires à partir des sections IPE - AIEP, IN - AINP et HEB - AHBP)
- Base de données des sections de l’entreprise Arcelor - ARCLRPro (sections à ouvertures hexagonales à partir des sections en I - CHXI et H - CHXH, à ouvertures hexagonales avec plaquettes intercalaires à partir des sections IPE - CHPI et H - CHPH, à ouvertures circulaires à partir des sections en I - CROI et H - CROH)
- Base de données des sections britanniques - UKSTPro (sections à ouvertures hexagonales à partir des sections UB - CUB et UC - CUC)
- Base de données des sections hollandaises - TSNLPro (sections à ouvertures hexagonales à partir des sections IPE - CIPE, HEA - CHEA et HEB - CHEB, à ouvertures hexagonales avec plaquettes intercalaires à partir des sections IPE - CIEP, HEA - CHAP et HEB - CHBP)