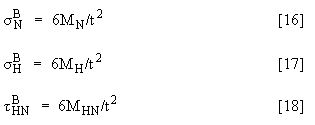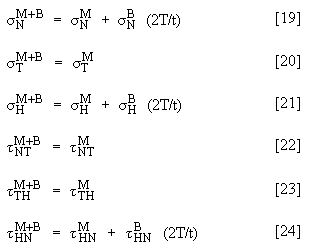In questa pagina è illustrato come vengono calcolate le sollecitazioni della membrana primaria e di flessione primaria (Pm e Pb).
Il calcolo di queste sollecitazioni implica l'esecuzione di diversi passaggi. Per iniziare, riproiettare i sei tensori di sollecitazione globale nel sistema di coordinate locale definito dalla linea di classificazione della sollecitazione (SCL). Quindi si integrano i sei tensori di sollecitazione locale, σN, σT, σH, τNT, τTH, τHN, lungo la SCL per ottenere il carico totale (FN, FT, FH, FNT, FTH, FHN) utilizzando:
Dove T è la posizione lungo la SCL.
Quindi è possibile calcolare la sollecitazione della membrana (F/A) per tutti e 6 i componenti. Per una SCL di lunghezza t,
Le sollecitazioni della membrana principali (
) vengono ottenute dal tensore i cui componenti sono specificati dalle equazioni 7-12. Queste sollecitazioni vengono ottenute riproiettando questo tensore nella direzione dell'asse principale.
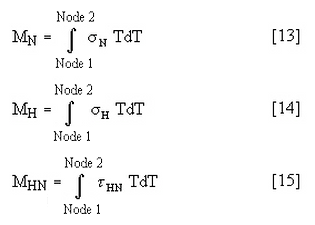
Successivamente verranno sviluppate le sollecitazioni di flessione sottraendo la sollecitazione della membrana dalla distribuzione della sollecitazione totale. Questa operazione viene eseguita punto di sollecitazione per punto di sollecitazione. Innanzitutto, sviluppiamo la distribuzione del carico del momento per una SCL di lunghezza t. Quindi, si integra la distribuzione del carico del momento per ottenere il momento sulla sezione trasversale.
Questi integrali devono essere calcolati utilizzando l'integrazione trapezoidale. I risultati successivi vengono utilizzati per calcolare la sollecitazione di flessione (MC/I) per una SCL di lunghezza t da:
Il passaggio successivo è calcolare la sollecitazione principale in corrispondenza di ciascuna estremità della SCL (
). Queste sollecitazioni di flessione e della membrana principali vengono ottenute dal tensore i cui componenti sono ottenuti mediante la sostituzione di T=Node 1 e T=Node 2.
Le sollecitazioni della membrana vengono ottenute dalle equazioni 7-12 e la sollecitazione di flessione dalle equazioni 16-18. Si noti che esistono due gruppi di sollecitazioni principali: uno in corrispondenza di T=Node 1 e un altro in corrispondenza di T=Node 2. Ancora una volta, le sollecitazioni principali vengono ottenute riproiettando il tensore nella direzione dell'asse principale.
A questo punto si dispone di tutte le sollecitazioni della membrana principali
e della somma delle sollecitazioni di flessione e della membrana principali.
Questi valori sono richiesti per determinare le quantità scalari di output:
- Pm e
- Pm + Pb
Questi due valori scalari vengono calcolati e generati in base a due diversi metodi di combinazione: sollecitazione di taglio massima e sollecitazione di Von Mises. Nella seguente tabella sono elencate le equazioni utilizzate per ciascun valore e metodo di calcolo:
| Tabella 1: Equazioni Pm e (Pm + Pb) per ciascun metodo di calcolo | |||
|---|---|---|---|
| Metodo di sollecitazione di taglio massima | Metodo di sollecitazione di Von Mises | ||
|
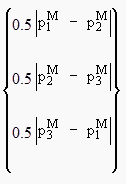
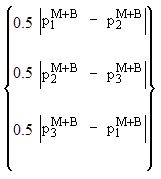
PM = più grande di:
|
[25] |
|
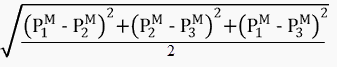
[27] |
|
(Pm + Pb) = più grande di:
|
[26] * |
|
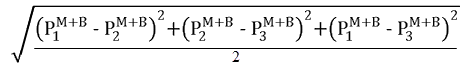
28 |
* Nota: le equazioni 26 e 28 devono essere valutate due volte, poiché esistono due gruppi di valori, uno in corrispondenza di T=Node 1 e un altro in T=Node 2. La quantità di output è basata sul nodo con il maggiore valore risultante.
Infine, l'intensità della sollecitazione di flessione primaria (Pb) viene calcolata dalla seguente semplice equazione della differenza per entrambi i metodi di combinazione delle sollecitazioni:
Pb = (Pm + Pb) - Pm[29]
Riferimento: ASME SGDA-99-2, PROPOSED NON-MANDATORY APPENDIX for Subcommittees III & VIII, Interpretation of Finite Element Analysis Stress Results, Rev 4, 2000.