進行性破損解析に対する収束の問題

ほとんどの進行性破損の問題で発生する共通の問題を解決します。

ほとんどの商用有限要素コードは、ニュートン-ラフソン アルゴリズムに基づく方程式ソルバーを採用しています。ニュートン-ラフソン アルゴリズムを使用する場合は、システムの非線形応答が十分にスムーズであるということを暗黙的に想定しています。システムの非線形応答が十分にスムーズで、ニュートン-ラフソン アルゴリズムを実際の解に十分に近い近似解を使用して開始したと仮定すると、ニュートン-ラフソン アルゴリズムは二次収束を示す一連の解を生成します(以下の図のパート A に定量的に示します)。

ただし、進行性破損の解析では、システムの非線形応答は、特に材料破損によって材料の構成挙動に大きな断続が生じるローカル レベルではスムーズになりません(たとえば、「一方向複合材料の損傷状態」セクションの図を参照)。このシステムの非スムーズな応答によって、非線形解析プロセスの収束特性はまったく異なったものになります。以下の図のパート B は、進行性破損の解析で遭遇する、非スムーズなシステムの解析の際に発生する収束の振る舞いの種類を定量的に示したものです。パート B に見られる最も重要な特性は、最大の残留力の大きさは、必ずしも平衡反復が実行されるときの連続的な減少を示すものではないということです。実際、最大の残留力の大きさは、突然残留力が消失して解が見つかったことを示すまで、比較的一定のままです。

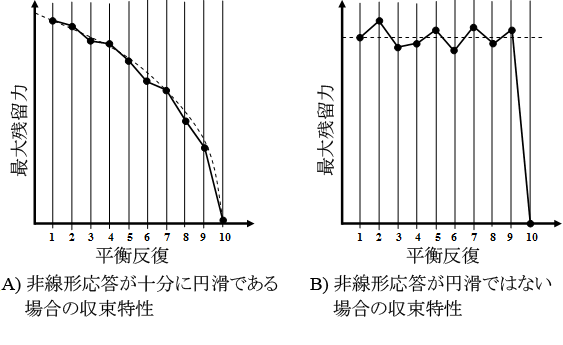
ほとんどの商用有限要素コードによって使用される既定の非線形解析戦略は、システムが上のパート A に示した収束特性を示すという仮定に基づいています。具体的には、商用有限要素コードでは平衡反復が実行されるときの最大残留力の大きさが、連続的で急速な減少を示すことが期待されます。残留力が平衡反復によって著しく減少していないように見える場合、商用有限要素コードは現在の時間増分に存在する非線形性の量が非常に大きいものと仮定します。従って、商用有限要素コードは、時間増分のサイズを減らすことによって、システムの応答に存在する非線形性の量を減らそうと試みます。この概念は、システムの非線形応答がスムーズでなく、残留力が連続した減少を示すことが期待されない進行性破損解析には適していません。実際、この方法を進行性破損解析に適用することは逆効果で、使用される時間増分が非常に小さくなり、解析を完了することが実質的に不可能になります。

Firehole Composites 社(現オートデスク)は、剛性の急速な劣化に関連する収束の課題を解決するため、アルゴリズムを自社開発して Helius PFA に実装してきました。Helius PFA を使用して材料剛性の劣化を提供する場合、有限要素コードは、進行性破損シミュレーションに対する安定した収束を示します。進行性破損解析における十分な経験から、有限要素コードでは、荷重増分のサイズを減らす必要があるのかを評価する前に、少なくとも 50 回の平衡反復の実行を許可することを推奨します。