母材の構成破損基準(一方向複合材料)
一方向複合材料の母材の構成破損基準を開発する際は、次の仮定を使用します。
- 母材破損は、母材の 6 つの平均応力成分
、
、
、
、
、
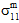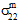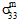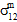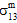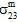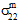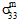のすべてに影響されると仮定されます。 - 母材の構成材料は横等方性であると仮定されるため、母材破損に対する および の影響は区別できません。また、母材破損に対する 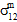および 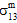の影響も区別できません。
- 母材破損の生成における母材の平均垂直応力(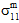、、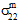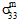)の影響は、垂直応力が引張か圧縮かによって異なります。
- 母材構成は横等方性であると見なされますが、母材破損は等方性イベントと仮定されます。つまり、母材破損の生成に寄与する応力成分の特定の組み合わせに関係なく、母材構成の剛性に対する母材破損の影響は同じです。具体的には、母材破損の発生時に、それぞれの母材平均係数(
、
、
、
、
、
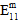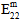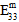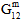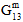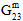)は、元の値のユーザ定義のパーセンテージ(既定値は 10%)まで低減する一方で、母材の平均ポアソン比(
、
、
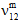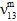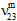)は変化しないと仮定されます。
これらの 4 つの基本的な仮定を使用して、ワイオミング大学とオートデスクの研究者は、母材の平均応力成分の二次関数として表される、次の母材破損基準を開発しています。
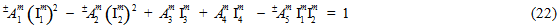
方程式 22 では、数量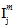 
(j = 1,2,3,4) は、母材の平均応力状態の横等方性不変量です。
数量 
(i = 1,2,3,4,5) は、母材破損基準の調整係数です。方程式 22 で、上付き記号 ± が調整係数 の前に置かれている場合、 の数値は関連する母材の平均応力が引張か圧縮かによって異なります。このため、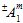
には可能な値が 2 つあることを示します。実際には、係数 
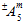には、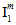
が正の値か負の値か、さらに 
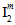が正の値か負の値かによって可能な値が 4 つあります。したがって、母材破損基準(方程式 22)には、複合材料の測定された強度を使用して決定する必要がある合計 10 個の調整係数が含まれています。
不変量を構成している母材の平均応力成分が合計の応力項になっていることに注意してください。つまり、機械的応力と熱応力の両方が含まれます。熱残留応力計算をアクティブにしている場合は、材料の硬化後冷却により生じた母材構成内の残留応力が、外部から適用されるどの機械的荷重や熱荷重よりも前に、合計の応力に明示的に含まれます。これらの残留応力は、繊維と母材構成とで熱膨張係数が違うことによって引き起こされます。通常、複合材料の硬化後冷却時には、母材構成は繊維構成よりも大きく収縮しようとします。したがって、母材構成は引張熱残留応力を示し、繊維構成は圧縮残留応力を示します。これらの熱残留応力がどのように決まるかの詳細については、「熱残留応力」のトピックを参照してください。