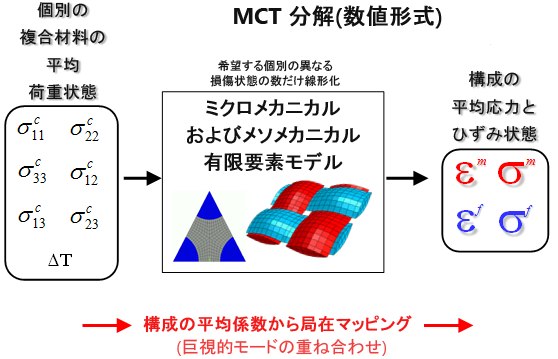
MCT 分解の数値形式

複合材料の有限要素モデルの使用に基づいた数値分解を説明します。

複合材料は、繊維構成と母材構成のみが含まれる単純な一方向繊維強化材料よりも複雑です。たとえば、織物複合材料および組物複合材料には、けん引と純粋な母材ポケット(つまり、メソ構成)の複数のファミリから構成されたメソ構造が含まれています。けん引のメソ構成は、ミクロ構成(繊維および母材)から構成されます。この場合、織物複合材料の平均応力とひずみ状態を、適切なメソ構成の平均応力とひずみ状態に分解する必要があります。さらに、メソ構成の平均応力とひずみ状態は、ミクロ構成(繊維および母材)の平均応力とひずみ状態に分解する必要があります。以前に説明したように、Helius PFA は解析の 2 分割化を使用して最終的な分解を実行します(「MCT 分解の解析フォーム」を参照)。ただし、解析の 2 分割化は、3 つ以上のメソ構成があるため、最初の分解(複合材料の平均値からメソ構成値へ)を実行するには実用的ではありません。3 つ以上のミクロ構成を含む複合材料の場合も、解析の 2 分割化は実用的ではありません。3 つ以上のメソ構成またはミクロ構成への分解には、Helius PFA は複合材料のメソ構造またはミクロ構造の有限要素モデルの使用に基づいた数値分解を使用します。

下図は、複合材料のメソ構造およびミクロ構造の高品質な有限要素モデルに依存した数値分解方法の概略図です。たとえば、平織物複合材料の数値解析方法では、織物複合材料のメソスケールの有限要素モデルの使用が必要となります。この織物複合材料では、反りけん引、充填けん引、母材ポケットの均質化された材料記述、つまり、3 つのメソ構成の有限要素モデルを使用します。均質化された個別の巨視的応力状態をメソスケールの有限要素モデルに適用でき、その結果として得られる解を、均質化された反りけん引、均質化された充填けん引、純粋な母材ポケットの平均応力とひずみ状態の計算に使用できます。これらのメソスケールの有限要素解を、反りけん引、充填けん引、母材ポケットのメソ構成の平均応力とひずみ状態に、巨視的応力成分とひずみ成分を直接マップする影響係数セットを計算するために使用できます。これらのメソ構成の影響係数セットは、織物複合材料が示す個別の損傷状態に対して決定されます。結果の係数は、構造レベルの進行性破損シミュレーション中に即座にアクセスできるように、材料データベースに格納されます。最後に、均質化された反りけん引と充填けん引の平均応力とひずみ状態を、解析の 2 分割化を使用して繊維と母材の平均応力とひずみ状態に分解できます。