Преобразование нагрузки в фиктивную массу

Предварительные замечания:

Нагрузки в подавляющем большинстве являются результатом действия сил тяжести (масс). При проведении динамических расчетов необходимо учитывать эти массы. Чтобы предоставить пользователю простое преобразование статических нагрузок (нагрузок силы тяжести) в фиктивные массы, в текстовом файле - анализаторе создана специальная команда "Активные массы" (MASses ACTive).

Указанное преобразование позволяет пользователю определять статические нагрузки только один раз - в процессе статического расчета - и затем использовать их в виде фиктивных масс вычислительной модели конструкции для выполнения любых типов динамического анализа.

Для успешного преобразования нужны два элемента. Первый – это набор направлений, в которых массы активны. Обычно используются все глобальные направления (X, Y, Z), так как только в специфических случаях силы инерции действует не по всем этим направлениям. Второй – это количество сил инерции. Оно определяется числом статических нагрузок и направлением нагрузок, которые учитываются во время преобразования. Дополнительно необходим специальный коэффициент, на который будет умножаться значение нагрузки.

Характер нагрузки автоматически преобразуются в фиктивные массы: сосредоточенные силы преобразуются в сосредоточенные массы, моменты – в моменты инерции масс, распределенные силы - в распределенные массы.

Синтаксис:

ANA [ DYN | MOD | TRAN | HAR | SEIsmic | SPEctral ], (все типы динамического расчета)

CASe (#<number> <name>)

MASess ACTive [X/Y/Z]

[X|Y|Z ] (MINus|PLus) <case_list> COEfficient=<c>

Прим.: Представленный выше синтаксис вводится только в текстовый файл и удаляется из файла данных после успешного сохранения в программе.

Основные правила:

Пусть r = r(x) - функция распределения плотности масс внутри данного элемента, а N(x) - матрица узловой интерполирующей функции (матрица функции формы). Матрица масс элемента создается в соответствии со следующей основной формулой 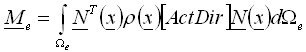(1) :

, (1)

где

Флаги активности общего направления устанавливаются командой MASess ACTive [X/Y/Z], т. е. любое направление активно. Эта команда - основа техники обработки масс в Robot в случае, когда некоторые компоненты сил инерции могут быть проигнорированы в процессе расчета.

Матрица масс будет создана из всех нагрузок, относящихся ко всем вариантам нагружения, заданным в списке вариантов <case_list>, и действующих на каждый элемент/узел согласно следующим правилам:

• каждая нагрузка из заданного варианта конвертируется в массу отдельно и независимо от других нагрузок и масс;
• в списке появляются только простые нагрузки (не комбинации!), для одной динамической нагрузки может быть задан список статических нагрузок, преобразуемых в фиктивные массы;
• общая матрица масс создается как сумма матрицы фиктивных масс от всех компонентов нагрузки и матрицы масс, состоящей из предварительно определенной собственной массы конструкции и/или заданных масс элементов. Часть матрицы масс, полученная из нагрузок, подвергается диагонализации, при этом может игнорироваться часть матрицы, содержащая моменты инерции масс.
• Значение функции плотности в данной точке получается как значение проекции текущего вектора силы f на вектор n з заданного общего направления

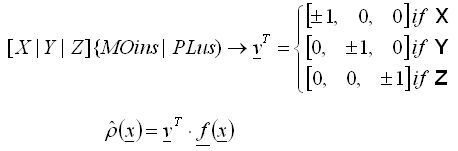  , (2)

• в каждой точке учитываются только положительные значения, следовательно

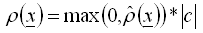  , (3)

  Прим.: Если не существует направления силы тяжести по умолчанию, спецификация направления должна быть сделана пользователем. Все направления, используемые для определения преобразования нагрузки в массы, должны быть приемлемы для заданного типа конструкции.
• Все направления используются для преобразования нагрузки в фиктивные массы, которые приемлемы для данного типа конструкции, так расчет плиты (PLAte) допускает только направление Z, для других типов конструкций приемлемыми могут быть только направления X и Y. Спецификации несовместимых направлений будут проигнорированы программой или появится сообщение об ошибке. Все типы трехмерных конструкций допускают все общие направления.

Пример:

Рассмотрим балку, нагруженную в центре нагрузкой в виде силы тяжести Fy= - 120 кН. Пусть статическая нагрузка, показанная ниже, имеет номер 3. Чтобы рассчитать формы свободных колебаний конструкции в варианте номер 10, учитывая массу (Fx=Fy= 12 232 кг), можно использовать следующую команду:

ANA MOD=3 MAS=CON

CAS #10 modal

MASses ACTive X Y

Y MINus 3

Подробности преобразования для различных типов нагрузок.

Нагрузки, действующие на балочные элементы:

• Распределенная нагрузка элемента.

  [Px= < px.>/Py=<py>/Pz=<pz>] (LOCal/GLObal) (PROjected) ([R=<r>])([R=<r>])

  Вектор плотности нагрузки преобразуется в основные направления, как задано формулой:

  (LOCal/GLObal) (PROjected) ([R=<r>]), учитывая флаг (PROjected) как для нагрузок, затем равные распределения масс устанавливается в соответствии с (2) (3)

• Постоянная нагрузка.

  Нагрузка собственного веса преобразуется в массу аналогично распределенной нагрузке элементов.

  Прим.: Эта операция должна использоваться с осторожностью, так как массы, полученные из нагрузки собственного веса, автоматически учитываются в динамических расчетах (если только плотность материалов больше нуля).
• Переменная нагрузка элементов.

  (X=<x1>)[ P=<p1>] ((JUSque)(X =<x2>)[P=<p2>] ) (R=<r>) (LOCal/GLObal) (RELative) (PROjected)

  Нагрузка преобразуется в соответствии с формулой:

  (LOCal/GLObal) (PROjected) ([R=

  затем устанавливается согласно (2)(3) распределенние масс.

  Прим.: Правило (3) включает следующую трактовку знаков для каждого компонента нагрузки отдельно , как показано на Р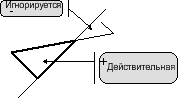ис.1.

  Рис.1

• Сосредоточенная сила элемента.

  [X=<x>] [F=<f>](R=<r>) (Local)(RELative)

  Общая масса m , сосредоточенная в точке x ₀ , вычисляется, исходя из общего представления вектора силы f , по формуле:

  , (4)

  Затем вычисляется согласованная матрица масс так, как если бы распределение масс было представлено дельта- функцией Дирака, сводящейся к:

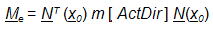  , (5)

• Сосредоточенный момент элемента.

  [X=<x>] [F=<fc>] (R=<r>) (LOCal)(RELative)

  Так как спецификация направления сил инерции не касается направлений вращательных сил инерции, то должно быть установлено отдельное правило выполнения преобразований между сосредоточенным моментом элемента и вращательной силой инерции определенного тела, присоединенного к элементу.

  Для того, чтобы получить вектор, относящийся к системе локальных координат элемента, преобразование вектора <fc> выполняется согласно настройкам (R=<r>) (LOCal). Чтобы избежать необходимости преобразования несовместимого типа вектора, нагрузка должна быть определена как LOCal и не R=<r>, иначе будет выдано предупреждение.

  Предполагается, что глобальные координаты совпадают с главными осями инерции тела, таким образом, компоненты вектора 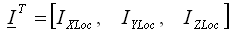представляют собой основные моменты инерции в глобальной системе координат. Из этого следует следующее ограничение моделирования: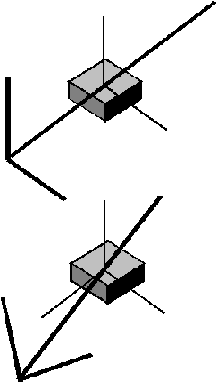

  Рис. 2

  Корректная ситуация.                 Некорректная ситуация, моделирование невозможно.

• Распределенный момент элемента.

  [M=<m>] (LOCal)

  В этой формуле <m> - вектор, который после преобразования векторного типа к системе локальных координат элемента представляет погонную плотность вращательной инерции, отнесенную к локальной оси элемента.

  Действуют все принципы, как для сосредоточенных моментов (см. Рис. 2).

Нагрузки, действующие на поверхностные элементы.

• Распределенная нагрузка элемента.

  [Px= < px.>/Py=<py>/Pz=<pz>]

  Рассчитывается вектор плотности нагрузки, который затем преобразуется в плотность масс в соответствии с (2)(3)

• Собственный вес конструкции.

  Нагрузка собственного веса преобразуется в эквивалентную унифицированную нагрузку и дальнейшие действия выполняются, как в предыдущем случае.

  Прим.: Эта операция должна использоваться с осторожностью, так как массы, полученные из нагрузки собственного веса, автоматически учитываются в динамических расчетах (если только плотность материалов больше нуля).
• Переменная нагрузка элементов.

  [P=<p1>] AU <n1>( [P=<p2>AU<n2> ([P=<p3> AU<n3>))

  В каждой точке интегрирования рассчитывается плотность нагрузки, которая затем преобразуется в плотность масс согласно (2)(3), см. Рис. (1). Усиленные правила интегрирования используются для

  NGAUS = 3x3 для Q8,

   = 7 для T6,

   = 2x2 для Q4 

   = 3 для T3

• Переменная нагрузка внутри контура.

  [P=<p1>] AU <n1>( [P=<p2>AU<n2> ([P=<p3> AU<n3>)) PROjected DIRection <v> _CONtour <l_node>

  В каждой точке интегрирования рассчитывается плотность нагрузки, которая затем преобразуется в плотность масс согласно (2)(3), см. Рис. (1). В случае, если не вся площадь элемента относится к контуру, то для достижения требуемой точности интегрирования. Внутри элемента выполняется полное автоматическое интегрирование с использованием до 100x100 точек сетки. Таким образом, применение этой опции может замедлять процесс расчета матрицы масс.

• Переменная нагрузка вдоль линии.

  LIN

  <n1>[P=<p1>] Jusque <n2> (P=<p2>) ( [LOCal (GAMma=<gamma>)] )

  Только поступательная сила может быть преобразована в массу , распределенную вдоль линии.

  В каждом сегменте линии, пересекающей элемент, используется 3-х точечная формула интегрирования Гаусса. Вектор плотности нагрузки преобразуется к системе глобальных координат, затем в соответствии с (2)(3) строится распределение масс вдоль линии.

• Сосредоточенная нагрузка в дополнительной точке.

  NODe (auxiliary)

  F=<f> ( [R=<r>] )

  Только поступательная сила может быть преобразована в массу элемента (для момента элемента балки - инерция вращательного преобразования позволена, а здесь запрещена). Вектор силы <f> преобразуется, если необходимо, к глобальной системе координат, затем согласно (2),(3) рассчитывается значение массы, приложенной в точке внутри элемента, далее в соответствии с (5) строится матрица масс. Элемент, к которому относится масса, находится автоматически. Элемент, к которому относится масса, находится автоматически.

Узловые нагрузки.

• Сосредоточенная сила.

  NODe

  F=<f> ( [R=<r>] )

  Чтобы получить значение узловой массы, вектор силы <f> преобразуется согласно (2),(3).

• Сосредоточенный момент.

  NODe

  F=<c> ( [R=<r>] )

  При определении направления сил инерции не рассматриваются направления вращательной инерции, так что для выполнения преобразования сосредоточенного узлового момента к моменту инерции определенного тела, прикрепленного к узлу, должно быть установлено отдельное правило.

  Преобразование типа вектора <fc> выполняется согласно (R=<r>) правилу получения вектора 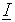, относящегося к глобальной системе координат. Чтобы не получить недопустимый тип преобразования вектора, не должно быть ни LOCal, ни R=<r>, иначе будет выдано сообщение об ошибке.

  Предполагается, что глобальные координаты совпадают с главными осями инерции тела, таким образом, компоненты вектора 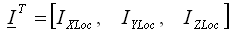представляют собой основные моменты инерции в глобальной системе координат.

  Прим.: Это правило отличается от правила, используемого в случае сосредоточенной массы, присоединенной к балочному элементу.