En ingeniería civil se utilizan varias curvas de transición para introducir gradualmente curvatura y peralte entre tangentes y curvas circulares, así como entre dos curvas circulares con curvatura diferente.
En su relación con otras tangentes y curvas, cada espiral es una curva de entrada o una curva de salida.
Los dos parámetros más utilizados por los ingenieros en el diseño y la disposición de una espiral son L (longitud de espiral) y R. El parámetro R hace referencia al radio de curvatura en un extremo de la espiral. R1 y R2 se pueden utilizar para diferenciar el radio al inicio y al final de la espiral.
La siguiente ilustración muestra los distintos parámetros de una espiral:
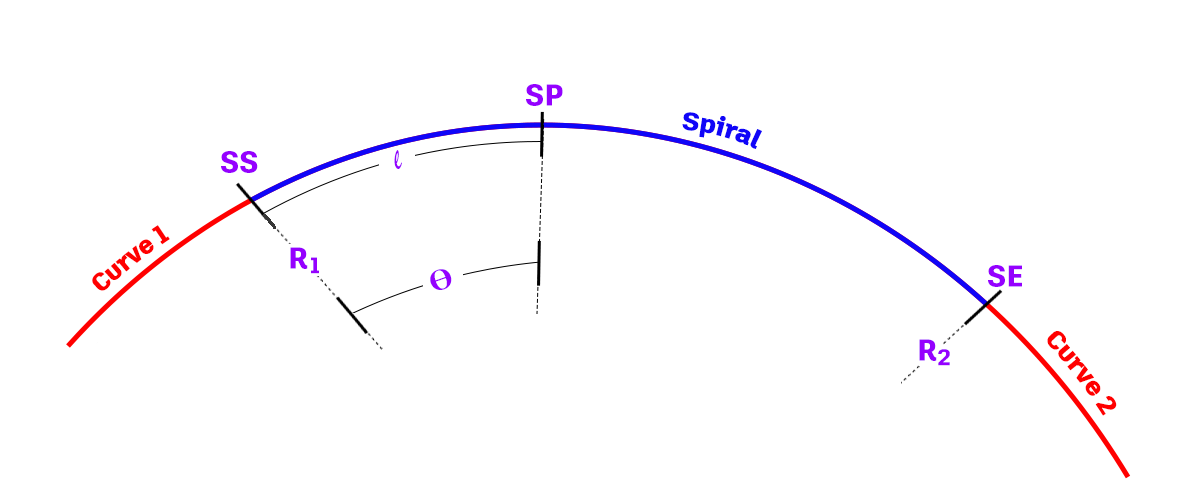
| Parámetro de espiral | Descripción |
| R1 | El radio de curva 1. |
| R2 | El radio de curva 2. |
| EE | Posición inicial de la espiral. |
| SE | Posición final de la espiral. |
| SP | El punto de espiral en la longitud de arco l. |
| Θ | El ángulo central en el punto espiral con la longitud de arco l. |
| l | La longitud de arco desde la posición inicial de la espiral a lo largo de la espiral. |
| L | Longitud total del arco de la espiral entre las posiciones inicial y final de la espiral. |
Espiral compuesta
Las espirales compuestas proporcionan una transición entre dos curvas circulares con radios distintos. Existen dos tipos de espiral: simple y compuesta. Una espiral compuesta consta de una curva compuesta de dos espirales simples. Contiene dos tramos, cada uno de los cuales es una espiral simple, que se une tangente continuamente con su espiral adyacente. Esto permite la continuidad de la función de curvatura y proporciona un modo de introducir una transición uniforme en el peralte.
Clotoide
Aunque Autodesk Civil 3D admite varios tipos de espiral, la clotoide es la más comúnmente utilizada. Este tipo de espiral se utiliza de forma universal tanto para el diseño de vías férreas como de carreteras.
Investigada inicialmente por el matemático suizo Leonard Euler, la función de la curvatura de la clotoide es una función lineal elegida de forma que su curvatura sea cero (0) como una función de longitud donde la espiral coincide con la tangente. A continuación, la curvatura aumenta linealmente hasta equipararse a la curva adyacente en el punto en el que espiral y curva coinciden.
A diferencia de la curva simple, también mantiene la continuidad de la curvatura local, lo que es cada vez más importante para los vehículos a velocidades más altas.
Fórmula
Las espirales clotoides se pueden expresar con las siguientes fórmulas: 
- Θ= el ángulo central en el punto espiral en la longitud de arco l.
- l = La longitud del arco a lo largo de la curva.
Planicidad de la espiral: 
Ángulo total subtendido por espiral: 
La distancia de tangente en el punto espiral-curva desde del punto tangente-espiral es:
La distancia de desfase de tangente en el punto espiral-curva desde del punto tangente-espiral es:
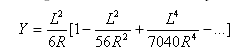
Espiral de Bloss
En lugar de utilizar la clotoide, se puede utilizar la espiral de Bloss como transición. Una ventaja de esta espiral sobre la clotoide radica en que el desplazamiento de P es menor y por tanto hay una transición mayor, con una extensión de espiral también mayor (K). Este factor es importante en el diseño del carril.
Fórmula
Otras expresiones clave:
La distancia de tangente en el punto espiral-curva desde del punto tangente-espiral es:
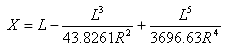
La distancia de desfase de tangente en el punto espiral-curva desde del punto tangente-espiral es:
Curvas sinusoidales
Estas curvas representan un rumbo coherente de curvatura y son aplicables a la transición entre 0 y 90 grados de desviación de tangente. Sin embargo, las curvas sinusoidales no se utilizan mucho porque son más empinadas que una espiral verdadera y, por lo tanto, más difíciles de tabular y jalonar.
Fórmula
- Θ= el ángulo central en el punto espiral con la longitud de arco i.
- l = La longitud del arco a lo largo de la curva.
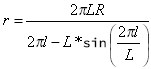
donde r es el radio de curvatura de cualquier punto dado.
Curva tangente en disminución de media onda sinusoidal
Este tipo de ecuación se utiliza normalmente en el diseño de vías férreas en Japón. Esta curva es útil en situaciones en las que se necesita una transición eficiente en el cambio de curvatura para ángulos de desviación pequeños (en relación con la dinámica del vehículo).
Fórmula
Una curva tangente en disminución de media onda sinusoidal se puede expresar de la siguiente manera:
donde 
y x es la distancia del inicio a cualquier punto de la curva y se mide a lo largo de la tangente inicial (extendida); X es el valor de X total al final de la curva de transición.
Otras expresiones clave:
La distancia de tangente en el punto espiral-curva desde del punto tangente-espiral es:
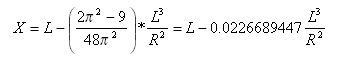
La distancia de desfase de tangente en el punto espiral-curva desde del punto tangente-espiral es:
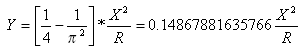
Parábolas cúbicas
Las parábolas cúbicas convergen con menor rapidez que las espirales cúbicas, por lo que su uso es más común en el diseño de carreteras y ferrocarriles.
Fórmula
Radio mínimo de parábola cúbica
Donde: Θ= El ángulo central en el punto espiral con la longitud de arco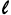 
.
Consulte el diagrama anterior como referencia.
Una parábola cúbica alcanza un r mínimo en:
De forma que 
El radio de una parábola cúbica disminuye desde el infinito hasta en 24 grados, 5 minutos, 41 segundos y de ahí en adelante comienza a aumentar de nuevo. Esto hace que las parábolas cúbicas resulten inútiles para desviaciones mayores de 24 grados.
Cúbica (JP)
Esta transición se ha desarrollado para satisfacer requisitos japoneses. Se han desarrollado una serie de aproximaciones de la clotoide para su uso en situaciones en las que sea necesario acomodar un pequeño ángulo de desviación o un radio mayor. Una de estas aproximaciones, utilizada para el diseño en Japón, se denomina cúbica (JP).
Fórmula
Cúbica (JP) se puede expresar de la siguiente manera:
Donde X = distancia de tangente en un punto espiral-curva desde el punto tangente-espiral
Esta fórmula también se puede expresar de la siguiente manera:
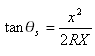
Donde 
es el ángulo central de la espiral (ilustrado como i1 e i2 en la ilustración)
Otras expresiones clave:
La distancia de tangente en el punto espiral-curva desde del punto tangente-espiral es:
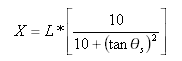
La distancia de desfase de tangente en el punto espiral-curva desde del punto tangente-espiral es:
Parábola cúbica NSW
Es un tipo de parábola cúbica modificada que cumple los requisitos de las normas de Nueva Gales del Sur (Australia).
Fórmula
La parábola cúbica NSW se puede expresar del modo siguiente:
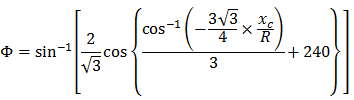
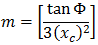
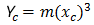
- Φ = ángulo entre línea radial final en R y línea perpendicular a la tangente inicial
- R = radio de curva
- Xc = total X de la espiral dada
- Yc = Y total de la espiral dada
Espirales bicuadráticas (Schramm)
Las espirales bicuadráticas (Schramm) tienen valores bajos de aceleración vertical. Contienen dos parábolas de segundo grado cuyos radios varían como una función de longitud de curva (l).
Fórmula de curva simple
Curvatura de la primera parábola:
para 
Curvatura de la segunda parábola:
para 
Esta curva se especifica mediante la longitud (L) definida por el usuario de la curva de transición.
Fórmulas de curva ovoide
Curvatura de la primera parábola:
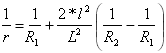para 
Curvatura de la segunda parábola:
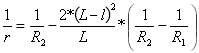para 