Az építőmérnökök különböző átmeneti íveket használnak. Ez azt a célt szolgálja, hogy két érintő és körív, illetve két eltérő görbületű körív esetén is fokozatos görbületet, illetve túlemelést tudjanak alkalmazni.
Más érintőkkel és ívekkel való kapcsolatát tekintve minden átmenetiív vagy bemenő-, vagy kimenőív.
A mérnökök által az átmenetiívek tervezéséhez és elkészítéséhez leggyakrabban használt két paraméter az L (átmenetiív hossza) és az R. Az R paraméter a görbületi sugárra vonatkozik az átmenetiív egyik végén. Az R1 és az R2 az átmenetiív elején és végén lévő sugár megkülönböztetésére használható.
A következő ábra az átmenetiívek különböző paramétereit szemlélteti:
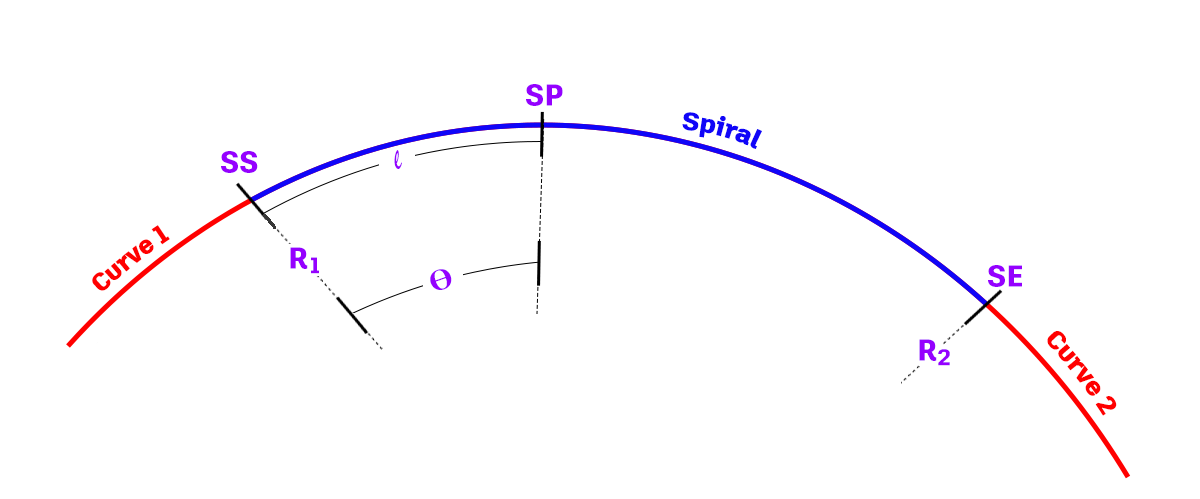
| Átmenetiív-paraméter | Leírás |
| R1 | Az 1. ív sugara. |
| R2 | A 2. ív sugara. |
| SS | Az átmenetiív kezdőpozíciója. |
| SE | Az átmenetiív végpozíciója. |
| SP | Az l ívhossznál lévő átmenetiív-pont. |
| Θ | A központi szög az l ívhossznál lévő átmenetiív-pontban. |
| l | Az átmenetiív kezdőpozíciójától mért ívhossz az átmenetiív mentén. |
| L | Az átmenetiív kezdő- és végpozíciója közötti átmenetiív teljes ívhossza. |
Kosár-átmenetiív
A kosár-átmenetiívek lehetővé teszik az átmenetet két eltérő sugarú körív között. Kétféle átmenetiív-típus létezik: egyszerű és összetett. A kosár-átmenetiívet két egyszerű átmenetiívből összeálló ívből alkotja. Két szakaszból tevődik össze, amelyek mindegyike egy-egy egyszerű átmenetiív, amely folyamatosan köti össze az érintőt a szomszédos átmenetiívvel. Ez lehetővé teszi, hogy folyamatos maradjon a görbületi függvény, és módot ad arra, hogy sima legyen a túlemelésátmenet.
Klotoid átmenetiív
Bár az Autodesk Civil 3D program az átmenetiívek több típusát is támogatja, a leggyakrabban használt típus a klotoid átmenetiív. A klotoid átmenetiívet világszerte használják autópályák és sínpályák tervezése során.
Ezt a görbét elsőként a Leonard Euler svájci matematikus vizsgálta meg. A klotoid görbületi függvénye olyan típusú, hogy az átmenetiív és az érintő találkozásánál a görbület zérus (0) értékű legyen. A görbület lineárisan növekszik egészen addig, amíg el nem éri a szomszédos görbe görbületi értékét abban a pontban, ahol az átmenetiív és az ív találkozik.
Az egyszerű ívekkel ellentétben a klotoid görbének a lokális görbülete is folyamatos, ami nagy sebességgel haladó járműveknél kiemelten fontos.
Képlet
A klotoid átmenetiívek a következő képletekkel fejezhetők ki: 
- Θ = A központi szög az l ívhossznál lévő átmenetiív-pontban.
- l = Az ív mentén mért ívhossz.
Átmenetiív lapossága: 
Az átmenetiív által bezárt teljes szög: 
Az egyenes távolság az átmenetiív-ív és az érintő-átmenetiív pontok között:
Az egyenes eltolási távolság az átmenetiív-ív és az érintő-átmenetiív pontok között:
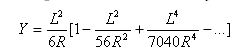
Bloss átmenetiív
A klotoid helyett a Bloss átmenetiív is használható átmenetként. Ennek az átmenetiívnek az az előnye, hogy az eltolt P értéke kisebb, ezért hosszabb az átmenet, és nagyobb az átmenetiív túlnyúlása (K). Ez a tényező sínpályák tervezésénél fontos.
Képlet
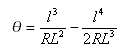
További fontos kifejezések:
Az egyenes távolság az átmenetiív-ív és az érintő-átmenetiív pontok között:
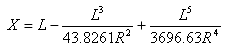
Az egyenes eltolási távolság az átmenetiív-ív és az érintő-átmenetiív pontok között:
Szinuszos ívek
Ezek a görbék konzisztens görbületi irányokat mutatnak, és a 0 és 90 fok közötti érintő iránytörések átmeneteként alkalmazhatók. A szinuszos ívek használata azonban nem gyakori, mivel meredekebbek, mint egy valódi átmenetiív, ezáltal nehéz azokat tabulálni és kitűzni.
Képlet
- Θ = A központi szög az i ívhossznál lévő átmenetiív-pontban.
- l = Az ív mentén mért ívhossz.
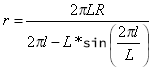
Ahol r a görbület sugara bármely pontban.
Eltűnő szinusz félhullám érintő ív
Ezt a képletet Japánban használják a vasúti pályák tervezése során. Ezt az ívet abban az esetben érdemes használni, ha a (jármű dinamikájához képest) kis iránytörési szögek esetén hatékony átmenetet kell létrehozni, mert megváltozik a pálya görbülete.
Képlet
Az eltűnő szinusz félhullám érintő íveket a következőképpen lehet kifejezni:
Ahol 
és x a kezdőponttól az ív bármely pontjáig, a (kiterjesztett) kezdeti érintő mentén mért távolság; X az átmeneti görbe végében a teljes X.
További fontos kifejezések:
Az egyenes távolság az átmenetiív-ív és az érintő-átmenetiív pontok között:
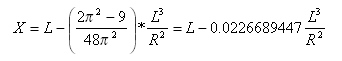
Az egyenes eltolási távolság az átmenetiív-ív és az érintő-átmenetiív pontok között:
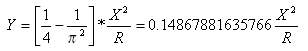
Harmadfokú parabola
A harmadfokú parabolák kevésbé intenzíven tartanak össze, mint a harmadfokú átmenetiívek, amely a vasút és autópálya tervezésben megkönnyíti azok használatát.
Képlet
A harmadfokú parabola minimális sugara
Ahol: Θ = A központi szög a(z)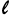 
ívhossznál lévő átmenetiív-pontban.
Referenciaként lásd a fenti ábrát.
A harmadfokú parabola itt éri el a minimális r sugarat:
Így 
A harmadfokú parabola sugara végtelentől kezdődően értékig, 24 fok, 5 perc, 41 másodperc szögig csökken, majd ettől kezdve újra növekszik. Emiatt a harmadfokú parabolák a 24 foknál nagyobb iránytörések esetén használhatatlanok.
Harmadfokú (JP)
Ezt az átmentet a Japánban érvényes követelményekhez fejlesztették ki. A klotoid görbék közelítésére számos módszert kifejlesztettek. Ezeket olyan esetekben lehet használni, amikor nem küszöbölhető ki egy kis iránytörési szög, vagy egy nagy sugár. Ezen közelítések egyike a Japánban használt Harmadfokú (JP).
Képlet
A Harmadfokú (JP) a következőképpen fejezhető ki:
Ahol X = az átmenetiív-ív pont és az érintő-átmenetiív pont közötti távolsággal
A képletet a következőképpen is le lehet írni:
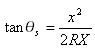
Ahol 
az átmenetiív központi szöge (az ábrán i1-gyel és i2-vel jelölve)
További fontos kifejezések:
Az egyenes távolság az átmenetiív-ív és az érintő-átmenetiív pontok között:
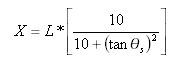
Az egyenes eltolási távolság az átmenetiív-ív és az érintő-átmenetiív pontok között:
NSW harmadfokú parabola
Ez egy, az New South Wales-i (ausztráliai) szabványoknak való megfelelés érdekében módosított harmadfokú parabola.
Képlet
Az NSW harmadfokú parabola a következőképpen fejezhető ki:
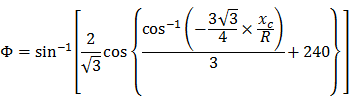
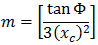
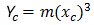
- Φ = az R-nél levő végső sugárirányú vonal és a kezdeti érintőre merőleges vonal által bezárt szög.
- R = az ív sugara
- Xc = az adott átmenetiív teljes X értéke
- Yc = az adott átmenetiív teljes Y értéke
Negyedfokú (Schramm) átmenetiívek
A negyedfokú (Schramm) átmenetiívek alacsony értékű függőleges gyorsulással rendelkeznek. Két másodfokú parabolából épülnek fel, amelyek sugara az ívhossz (l) függvényében változik.
Egyszerű ív képlete
Az első parabola görbülete:
ahol 
A második parabola görbülete:
ahol 
Ez az ív az átmeneti körív felhasználó által megadott hosszúságából (L) adódik.
Kosárív-képletek
Az első parabola görbülete:
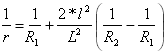ahol 
A második parabola görbülete:
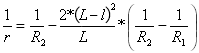ahol 