Um problema de valor próprio generalizado é definido da seguinte maneira:
K φ - λM φ = 0
em que K, M indicam rigidez e matrizes de massa, respectivamente, {φ, λ} – pares próprios (modo de vibração natural e valor próprio).
Dois tipos de vetores residuais são definidos:
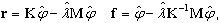
em que {φ, λ} designa pares próprios calculados que incluem determinados erros de cálculo. A primeira expressão define um vetor residual em termos de forças, enquanto a segunda define um vetor residual em termos de deslocamentos.
São aplicados três critérios diferentes de estimativa de erros de cálculo para vetores próprios:
Métodos
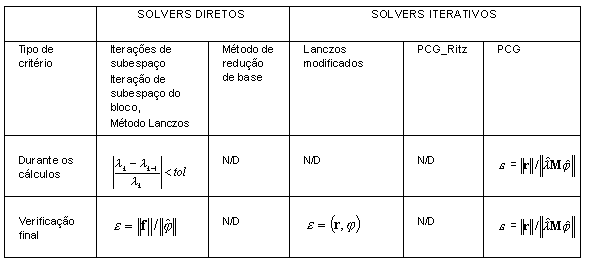
Comentários
- A precisão durante os cálculos de estrutura para os métodos Lanczos e Lanczos modificado (solver iterativo) do pseudomodo não é determinada. Somente a verificação final é executada.
- É realizada a verificação de convergência
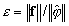em cada uma das 20 etapas do método de Lanczos para o modo sísmico. O parâmetro de tolerância na caixa de diálogo Parâmetros de análise modal é ignorado. - A redução de base e o PCG_Ritz são os métodos de Ritz. A verificação de precisão não é executada. O parâmetro de tolerância na caixa de diálogo Parâmetros de análise modal é ignorado.
- O método PCG do solver iterativo aplica os critérios de convergência mais rigorosos
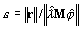durante os cálculos. O parâmetro de tolerância na caixa de diálogo Parâmetros de análise modal – Solver iterativo define o limite superior para ε; portanto, ε ≤ tol é uma condição para interações de parada.
A precisão não deverá ser confundida com a tolerância determinada na caixa de diálogo Parâmetros de análise modal ao usar o solver direto esparso ou solver de linha de horizonte se o modo modal estiver selecionado. A tolerância durante os cálculos é definida de acordo com a fórmula a seguir.
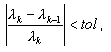
em que λk, λk-1 – dois valores próprios sucessivos nas etapas de iteração k, k-1 e tol indica a tolerância, adotada na caixa de diálogo Parâmetros de análise modal. A determinação da precisão final dos cálculos (1-3) é demorada e executada no estágio final da análise modal para verificar a precisão obtida. Diminuem a tolerância tol para aumentar a precisão dos cálculos, o que aumenta o número de iterações.
Se a precisão de alguns modos após os cálculos for insuficiente, será necessário o seguinte.
|
SOLVERS DIRETOS |
SOLVERS ITERATIVOS |
|||
|---|---|---|---|---|
|
Iterações de subespaço, iterações de subespaço de blocos, método de Lanczos |
Método de redução de base |
Lanczos modificado |
PCG_Ritz |
PCG |
|
Diminuem a tolerância na caixa de diálogo Parâmetros de análise modal |
Aumentam o número de nós de base e direções de base |
Diminuem a tolerância na caixa de diálogo Parâmetros do solver iterativo e aumentam o número de modos |
Aumentam o número de modos |
Diminuem o valor da tolerância na caixa de diálogo Parâmetros de análise modal |
Consulte também: