Suposições da análise modal

A análise modal determina valores próprios e valores derivados (pulsações próprias, frequências naturais ou períodos próprios), precisão, vetores próprios, coeficientes de participação e massas de participação para o problema das vibrações próprias estruturais.

Estão disponíveis três modos de análise dinâmica de estrutura (modal, sísmico e sísmico (pseudo)).

Os valores próprios e os modos próprios são obtidos com base na fórmula a seguir.

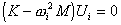(1)

em que:

K – matriz de rigidez da estrutura.

M – matriz de massa da estrutura.

ω_i – pulsação natural (frequência circular natural) do modo “i”.

U_i – vetor de modo próprio do modo “i”.

O número de modos próprios a serem considerados pode ser especificado da forma a seguir.

• O limite superior da pulsação, frequência ou período.
• O limite inferior da soma das massas de participação (porcentagens) ou como um número real de modos necessários.

Se o número do modo não for especificado, o valor padrão definido em Preferências será usado na análise.

Os parâmetros de controle para o algoritmo de problema próprio são os seguintes.

• Precisão dos cálculos (quantidade de erros).
• Número máximo de interações.

Os seguintes tipos de matriz de massa estão disponíveis.

• Consistente (matriz consistente – sempre com relação aos graus de liberdade rotacionais),
• Fragmentado com rotações (matriz diagonal – com relação aos graus de liberdade de rotação),
• Fragmentado sem rotações (matriz diagonal sem graus de liberdade rotacionais).

As matrizes de massa fragmentada Mlum são criadas de acordo com a regra:

Mlum(i,j) = 0,0 ; para i≠j

Mlum(i,j) = Stot/Sdiag * M(i,j) ; para i=j (2)

em que:

Stot – Soma de todos os elementos da matriz de massa consistente M.

Sdiag – Soma de elementos diagonais da matriz de massa consistente M.

Portanto, a massa do elemento é preservada e a matriz de massa do elemento é definida positivamente.

Os vetores próprios nos módulos de resultado são normalizados de forma que o termo máximo de cada vetor seja igual a 1,0.

Os vetores próprios internos usados durante os cálculos são normalizados para que

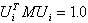(3)

O valor de precisão exibido na caixa de diálogo Valor próprio é considerado como uma precisão de convergência obtida. Esse valor é uma quantidade de erro aceitável para a precisão com que o valor próprio λ_i e o vetor próprio U_i obtido durante a iteração para o modo de ordem i satisfazem a equação de problema próprio:

K * U_i = λ_i * M * U_i (4)

Os coeficientes de participação estão definidos como:

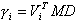
em que:

D – Vetor unitário definido como segue:

D(j) = 1,0 se j for igual ao grau de liberdade de ordem i

D(j) = 0,0 se j ¹ i,

V_i – O vetor próprio do modo i normalizado na forma que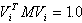

As massas de participação são dinâmicas, participando no movimento da estrutura para cada modo e cada grau de liberdade. São consideradas as massas atuais para o modo atual e como as massas relativas que são a soma das massas atuais do primeiro modo para o atual. Os valores são apresentados como uma porcentagem do total de massas dinâmicas.

As massas de participação atuais são definidas como segue:

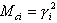
Atualmente, o algoritmo de Lanczos, que constitui uma abordagem poderosa para resolver problemas de valor próprio em grande escala (1), é o método padrão para encontrar a solução para o problema próprio. Ele encontra os n valores próprios e os vetores próprios necessários com qualquer precisão.

Na maioria dos casos, o Método de Lanczos é preferível como o mais adequado. No entanto, as restrições a seguir se aplicam.

• A matriz tridiagonal T não deve ser de um tipo consistente.
• A matriz de massa M deve ser tratada como Fragmentada com rotações ou Consistente. Quando Fragmentada sem rotações é selecionada, a matriz de massa é automaticamente agregada como Fragmentada com rotações.

Nota: Para estruturas separadas, não é possível usar o Método de Lanczos porque uma matriz tridiagonal T de um tipo não consistente é necessária, enquanto uma matriz T de estrutura separada é de um tipo consistente.

Quando em um programa, um método de Lanczos é selecionado, o programa altera um método de cálculo para um método de iteração de subespaço. Para usar o método de Lanczos em cálculos, estruturas separadas devem ser conectadas de forma que um modelo de estrutura não seja alterado (por exemplo, uma barra entre os suportes deve ser adicionada).

A redução a seguir da matriz tridiagonal T se aplica ao Método de Lanczos.

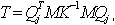
em que

Q_j = {q₁, q₂, ... , q_j} – matriz retangular Neq x j, Neq – número de equações, j – número de passos de Lanczos, q_j – vetor de Lanczos de ordem j.

A fórmula

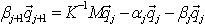
é usado para gerar o próximo vetor de Lanczos q _j+1 e define a linha atual da matriz T.

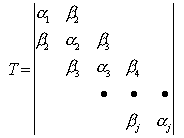
Portanto, o problema próprio reduzido é:

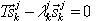, k=1,2,…,j

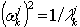, em que ω_k ^j é a aproximação de ordem j para ω_k, k=1,2,…,n, e n é o número necessário de valores próprios e vetores próprios. Um algoritmo continuará os cálculos (aumentando o j – número de passos de Lanczos) até que a precisão necessária para todos os n valores próprios seja alcançada.

O procedimento de ortogonalização dá suporte ao nível necessário de ortogonalidade entre os vetores de Lanczos, assegurando a segurança e a estabilidade numérica dos cálculos.

Os vetores próprios devem ser obtidos com as seguintes fórmulas:

U = Qs.

Método de redução de base

O método de redução de base obtém valores aproximados dos primeiros valores próprios, desde que alguns dados sobre eles já estejam agrupados. Esse método requer a atribuição de graus de liberdade principais (MDOF) para obter o sistema reduzido. O controle da criação do modelo reduzido é então possível e graus de liberdade indesejados podem ser excluídos do modelo reduzido, o que resultará em um sistema significativamente menor. É especialmente útil para aqueles com alguma experiência em análise dinâmica de estrutura e quando o comportamento da estrutura dinâmica é conhecido.

As regras a seguir se aplicam a esse método.

• MDOF deve ser especificado (nós e direções principais). Presume-se que somente deslocamentos (não rotações) possam ser atribuídos como graus de liberdade principais.
• É possível usar qualquer tipo de matriz de massa no algoritmo. No entanto, o tipo de matriz Fragmentada sem rotações garante o período de cálculo mais curto.
• A verificação de Sturm indica o número de frequências ignoradas. Esses valores e vetores próprios não serão encontrados. A única forma de encontrar a convergência de verificação é aumentar o número de MDOF para resolver o problema e comparar valores próprios.

O método inclui a transformação do grande problema próprio para o modelo FEM.

K U – ω² M U = 0 para o problema próprio para um modelo reduzido:

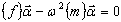
em que {f} – matriz de influência, {m} – matriz generalizada para o modelo reduzido.

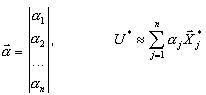
A base para essas transformações são as soluções obtidas para estados de unidade apropriados:

as forças nodais de unidade são aplicadas consequentemente para cada nó do tipo principal na direção selecionada do tipo principal. O problema estático de grande escala foi resolvido para n lados direitos:

K X_i ^* = T_i , i = 1, 2, …, n

em que T_i – vetor de carga correspondente à força de unidade de ordem i. Os nós e direções do tipo mestre devem ser definidos, todas as outras operações serão executadas automaticamente. Em seguida, o problema próprio reduzido é resolvido com o método de Jacobi. Como resultado, os valores aproximados de frequências w_i e dos vetores próprios U_i ^* , i=1,2,...,n são obtidos.

Consulte também:

Análise modal – Precisão dos cálculos na análise modal estrutural