Selecione entre os seguintes tipos de geometria e parâmetros de laje:
|
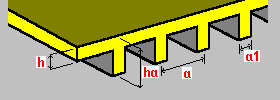
Nervuras unidirecionais de uma face: h – espessura da placa ha – altura da nervura a – espaçamento da nervura a1 – largura da nervura |
|
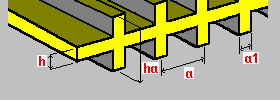
Nervuras unidirecionais de duas faces: h – espessura da placa ha – altura da nervura a – espaçamento da nervura a1 – largura da nervura |
|
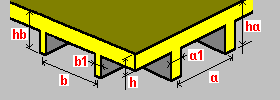
Nervuras bidirecionais de uma face: h – espessura da placa ha – altura da nervura hb – altura da nervura a – espaçamento da nervura a1 – largura da nervura b – espaçamento da nervura b1 – largura da nervura |
|
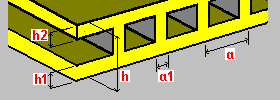
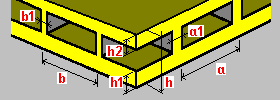
Piso de caixa unidirecional: h – espessura do piso h1 – espessura da placa inferior h2 – espessura da placa superior a – espaçamento da nervura a1 – largura da nervura |
|
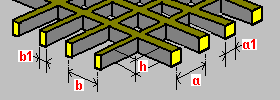
Piso de caixa bidirecional: h – espessura do piso h1 – espessura da placa inferior h2 – espessura da placa superior a – espaçamento da nervura a1 – largura da nervura b – espaçamento da nervura b1 – largura da nervura |
|
Grelha: h – altura da nervura a – espaçamento da nervura a1 – largura da nervura b – espaçamento da nervura b1 – largura da nervura |
|
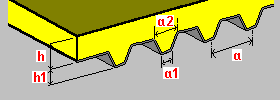
Laje em uma placa trapezoidal: h – espessura da placa h1 – altura da placa de aço a – espaçamento da nervura da placa de aço a1 – largura da nervura inferior a2 – largura da nervura superior |
|
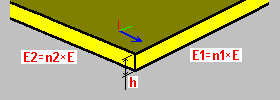
Ortotropia do material: h – espessura da placa n1 – coeficiente de rigidez n2 – coeficiente de rigidez |
|
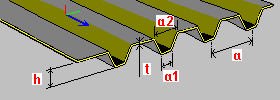
Placa trapezoidal: h – altura da placa t – espessura da placa a, a1, a2 – cotas de um segmento de placa única (valores de espaçamento, largura) |
|
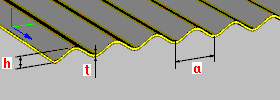
Placa corrugada: h – altura da placa t – espessura da placa a – cota de um segmento de placa única (espaçamento) |
|
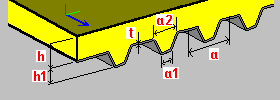
Laje composta com uma placa trapezoidal h – espessura da laje h1 – altura da placa t – espessura da placa a, a1, a2 – cotas de um segmento de placa única (espaçamento, larguras) Es – módulo de Young (aço trapezoidal) X – coeficiente de Poisson (aço trapezoidal) Eb – módulo de Young (concreto; um valor adotado com base no material selecionado) vb – coeficiente de Poisson (concreto; um valor adotado com base no material selecionado) |
|
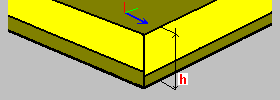
Espessura constante com rigidez reduzida: h – espessura da laje coeficientes de redução dos elementos da matriz: rigidez da membrana D, rigidez da flexão K e rigidez do cisalhamento H; além disso, é possível definir um coeficiente de redução de peso considerado durante a geração de uma carga de peso próprio; os valores desses coeficientes são definidos na caixa de diálogo Coeficientes de rigidez, peso, massa que é aberta após clicar em Coeficientes. |
|
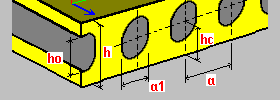
Laje vazada (com aberturas circulares ou ovais) h – espessura da laje a – espaçamento do enrijecedor, espaçamento da abertura a1 – largura da abertura/diâmetro do círculo ho – altura da abertura (laje com aberturas ovais) hc – distância entre o centro da abertura e a aresta da laje h1 – altura do flange inferior da laje h2 –altura do flange superior da laje (h2 = h - hc - c/2 - a1/2) c = ho - a1 (laje com aberturas ovais) A opção Ignorar rigidez da dobra transversal permite omitir ou considerar a rigidez da dobra K_YYYY nos cálculos. Ignorar rigidez da dobra (direção Y) visa a uma melhor modelagem das lajes vazadas pré-moldadas. |
A ortotropia do material introduz uma rigidez diversificada da placa resultante de diferentes propriedades físicas em direções perpendiculares. Uma diferença de rigidez é determinada por meio dos módulos de Young modificados E1, E2, respectivamente, na direção x, y da ortotropia selecionada. Os módulos E1, E2 são um produto de um material selecionado e dos coeficientes definidos pelo usuário n1, n2. Para ambas as direções, a relação da constante de Poisson é adotada. É possível usar esse tipo de ortotropia para criar um modelo de lajes de CA com armadura bidirecional.
É possível definir o coeficiente de rigidez das lajes de CA com armadura bidirecional com base na fórmula a seguir. Presumindo que o material da laje seja linearmente elástico, o coeficiente de rigidez para a direção paralela à direção da armadura é igual a:
n = 1+ 12/(h*h) * e*e * m * u / (1+ m*u)
em que:
h é a altura de uma seção de laje.
m = Ez/Eb é a relação entre o módulo de Young de aço e concreto.
e é a distância entre o centro de gravidade da armadura e o plano médio de uma laje.
u é a relação de armadura, expressa como uma fração decimal (uma área de seção de barras de armadura referenciada para uma área de unidade de uma seção de laje).
Consulte também: