Análise modal que reconhece forças estáticas – descrição e exemplo

As forças estáticas aplicadas a uma estrutura influenciam a frequência de vibrações da estrutura. A análise modal comumente usada (determinando as vibrações de uma estrutura) não reconhece a influência de forças estáticas. Para aproximar as condições reais em que uma estrutura funciona, os cálculos executados no Robot podem ser executados de acordo com a análise modal reconhecendo as forças estáticas aplicadas na análise modal.

Há dois estágios de cálculos de vibração da estrutura que reconhecem a operação de forças estáticas. Essas análises são de correlação estática entre tensão e deformação sob a influência de uma carga estática definida.

Estágio um: linear

em que:

x_st – Vetor desconhecido do estado estático

b – Vetor de uma carga estática definida (vetor de carga estática)

K – Matriz de rigidez

L (x_st, b) – Operador não linear

O vetor de carga estática b pode ser um caso de carga simples ou uma combinação de casos de carga definidos.

Estágio dois: análise modal (não linear)

, ( 2a )

em que:

K_s – Matriz de rigidez de tensão, originada das tensões no estado estático

M – Matriz de massa

ω_i² – Valor próprio (ω_i = pulsação)

Φ – Vetor próprio

Para resolver um problema estático não linear (modal), são usados os mesmos métodos que na análise estática não linear. Para um problema estático linear, a seguinte correlação contém: , em que G é uma matriz de rigidez geométrica.

Os valores positivos ω_i (ω_i > 0) descrevem estados estáveis de equilíbrio, enquanto os valores negativos (ω_i < 0) correspondem aos estados não estáveis de equilíbrio. Por sua vez, o valor zero (ω_i = 0) indica falta de estabilidade (flambagem).

Se a matriz K + K_s (x_st) parar de ser positivamente determinada, a carga estática se aproximará do valor crítico (flambagem). Durante a análise do problema estático não linear (modal), a convergência não é obtida. Se a abordagem linear (um estágio de análise estática) estiver selecionada e a matriz não for positivamente determinada, recomenda-se parar o cálculo, já que cálculos adicionais não fazem sentido.

Nota: Se a estrutura tiver elementos de cabo ou elementos do tipo de tensão de compressão, será fornecida a possibilidade de calcular tal estrutura somente de acordo com a abordagem não linear fornecida.

Exemplo

Considere o exemplo da estrutura mostrada no desenho a seguir. N refere-se a uma carga estática.

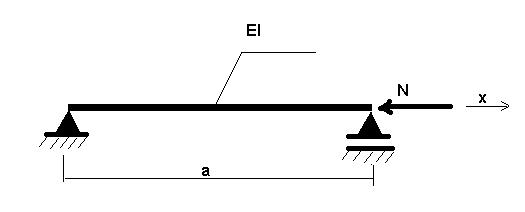
A fórmula a seguir descreve seu comportamento.

, ( 3 )

em que:

w – Deslocamentos devido à flexão

ρ – Densidade do material

F – Área de seção transversal

A solução para essa fórmula será pesquisada por meio da seguinte fórmula:

( 4 )

Uma vez que a expressão ( 4 ) é introduzida na fórmula ( 3 ), o seguinte é obtido.

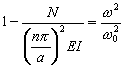, ( 5 )

em que:

– carga de flambagem

ω₀² – Valor próprio para o resultado N=0 da análise modal regular).

Após transformar a fórmula final, é obtido o seguinte.

, ( 6 )

em que ω² – Valor próprio obtido para a estrutura que passa pela operação da carga estática N.

O resultado das considerações acima é apresentado graficamente no desenho a seguir.

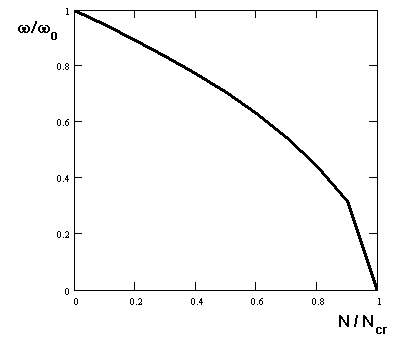
Em conclusão, para estruturas reais, a correlação ω= ω(b) é normalmente ligeiramente mais complexa que o obtido com a fórmula (6).