O método de iteração de subespaço do bloco é usado para resolver o problema de valor próprio generalizado.
Problemas de valor próprio generalizados são enfrentados durante a análise modal ou de flambagem de uma estrutura.
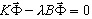
Problema de valor próprio generalizado (1)
- K representa a matriz de rigidez.
- B = M – matriz de massa no caso de análise dinâmica; nos casos restantes B = Ks, em que Ks é a matriz de rigidez de tensão, originada na linearização do operador não linear apropriado no caso de análise de flambagem.
- λ representa o valor próprio.
- Φ representa o vetor próprio.
O método de iteração de subespaço do bloco é preferível ao obter um número considerável de pares próprios (valores próprios e vetores próprios) para uma estrutura. Normalmente, esse número é superior a dez.
O método de iteração de subespaço do bloco funciona com todos os tipos de matrizes de massa, ou seja, consistente, fragmentada com rotações ou fragmentada sem rotações. A faixa de aplicação é limitada à análise modal. Selecionar Lanczos ativa os dois modos restantes: pseudomodal e sísmico.
A opção Verificação de Sturm determina os valores próprios ignorados durante o processo de verificação.
O método de iteração de subespaço do bloco consiste em iterações simultâneas de um vetor no subespaço com uma determinada dimensão. Cada vetor para o qual o processo de convergência foi executado é removido do subespaço de trabalho e um novo vetor inicial é adicionado em seu lugar. A ortogonalidade dos vetores é assegurada em cada etapa iterativa. O seguinte critério de convergência é aplicado:
![]() ( 2 )
( 2 )
em que:
i, k – número de um modo e número da etapa de iteração, respectivamente
tol – tolerância, definida no campo de edição “Tolerância”.
Os resultados das análises modais e de flambagem são determinados com certa precisão, determinada pela seguinte fórmula:
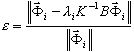 ( 3 )
( 3 )
Se o processo de convergência for lento, será recomendável aplicar o procedimento de deslocamentos na análise modal:
![]() ( 4 )
( 4 )
em que:
Kσ = K - σ M.
σ – valor de deslocamento.
O número de iterações entre dois deslocamentos sucessivos é tratado como o parâmetro desse procedimento.
O procedimento de deslocamento não deve ser aplicado à análise de problemas de flambagem porque há o perigo de deslocar os espectros de valores próprios na direção de carga crítica negativa (possivelmente descartando cargas críticas positivas) quando há valores próprios negativos para a estrutura.
Os pares próprios determinados são classificados da seguinte forma | λ1 | ≤ | λ 2 | ≤ ... ≤ | λ n |, o que resulta na localização dos parâmetros mínimos de carga crítica na parte superior da tabela com resultados.
Consulte também: