动态运动仿真分析理论

此理论背景同时适用于动态运动仿真和准静态运动仿真。

运动仿真结合了胡克定律 (F=-kx) 和牛顿第二定律 (F=ma) 的原理。通过消除力术语，在合并这两个方程式后，我们实现了 ma + kx = 0。现在，我们可以添加阻尼效应 (F=-cv) 以实现运动的一般方程式：

ma+cv+kx = 0

其中，m 是质量，a 是加速度，c 是阻尼系数，v 是速度，k 是刚度，x 是位移。在矩阵形式中，此方程式表示为：

[M]{a} + [C]{v}+[K]{x} = 0

从该基本方程式中，可以使用位移矢量 {x} 和控制材料响应的本构关系来确定应力和应变。

中心差分时间积分

运动仿真使用基于中心差分时间积分算法构建的显式求解器。该算法使用之前两种状态的知识来直接对当前状态（位移、速度和加速度）进行求解。从一种状态到下一种状态之间时间步长的大小由稳定时间增量（也称为 Courant 稳定性限制）来驱动。稳定时间增量控制允许的最大时间步长，超出该限制，解将放大。当考虑阻尼效应时，这表示为：

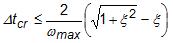
其中，Δtcr 是稳定时间增量，ωmax 是网格中的最大固有频率，ξ 是最高模式下临界阻尼百分比。

总而言之，运动仿真中的稳定时间增量非常小。幸运的是，显式求解器非常有效，可以相对轻松地处理材料和接触非线性，因为无需在每次迭代时都建立刚度矩阵。节点加速度可以直接求解。