模态频率理论背景
通过有限元分析确定固有频率和相应振型所依据的数学流程很复杂。为使理论更易于理解,我们将考虑包含一个自由度 (DOF) 的非常简单的线性弹簧质量系统。即,质量仅在一个方向上自由移动。
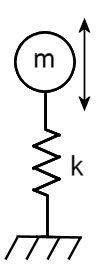
在下图中,m 是质量,k 是弹簧的刚度:
Hooke 定律定义使刚度为 (k) 的弹簧移动 (X) 距离所需的力 (F):
(1) F = k·X
牛顿第二运动定律指定单一自由度系统的力 (F)、质量 (m) 和加速度 (a) 之间的关系:
(2) F = m·a
结合这两个方程式,我们得到质量 (m)、加速度 (a)、弹簧刚度 (k) 和位移 (X) 之间的关系:
(3) m·a = k·X
以下方程式针对此简单的线性弹簧质量系统提供了振动的角频 (ω),单位为 弧度/秒:
(4) ω = (k/m)1/2
每个振动周期有 2 弧度。因此,接下来的方程式为我们提供振动的固有频率 (fn),单位为赫兹:
(5) fn = (k/m)1/2 / (2·π)
在实际的有限元模型中,由于网格中所有节点和单元的存在,我们将拥有三维运动和多个自由度。
注意:我们在固有频率计算中不考虑阻尼。阻尼是指因系统能量的消耗导致振幅的减小。能量消耗在克服摩擦力、粘滞力或其他阻力上。在典型制造材料(例如钢、铝和混凝土)中出现的阻尼量很小。因此,无阻尼的固有频率与实际的固有频率通常相差不多。相对于无阻尼系统,阻尼可减小振动频率。
在连续的系统中,有无限数量的振动模式。但是,在有限元模型中,存在有限数量的自由度,因此振动模式的数量也有限。确定这些复杂三维系统的振动频率和振型涉及矩阵运算、特征值和特征矢量。
方程式 (4) 是具有有限数量解的特征值和特征矢量问题。角频 (ω) 是一个标量。对于任何特定解,所有自由度均以相同角频振动。但是,振动的振幅 (δ) 是一个矢量。在我们的复杂系统中,δ 类似于我们单一自由度示例中的位移 (X)。不同自由度使用由 δ 的分量指定的振幅振动。此振幅变化为我们提供了振型。
特征值和特征矢量的正确定义以及用于模态分析求解的数学运算超出了本主题的讨论范围。