Theoretischer Hintergrund zu hyperelastischen Materialien
Die nichtlinearen Spannungs-Dehnungs-Merkmale von hyperelastischen Materialien, z. B. Gummi, sind komplex. Die zahlreichen verfügbaren Materialsorten variieren stark in ihrem Verhalten. Bei nichtlinearen Simulationen in Fusion werden hyperelastische Materialien mit dem Mooney-Rivlin-Materialmodell (Standard mit zwei Konstanten) dargestellt. Die Materialkoeffizienten werden durch die Kurvenangleichung experimentell erlangter Spannungs-Dehnungs-Rohdaten abgeleitet. Diese Daten können auf verschiedenen Tests beruhen, einschließlich der folgenden Spannungs-/Druck-Testbeispiele:
- Uniaxial (1 und 2)
- Eben
- Äqui-biaxial
- Biaxial
- Beschränkt
- Triaxial
- Volumetrisch
Die Beschreibung dieser Tests und die Rohdaten, die erzeugt werden, gehen über den Umfang dieses Themas hinaus. Die Materialtests werden durch spezialisierte Labors vorgenommen, die Kurvenangleichung muss außerhalb von Fusion durchgeführt werden. (Das Programm verfügt über keine integrierte Funktion zum Empfangen der Rohdaten und Durchführen der Kurvenangleichung.) Es gibt verschiedene Programme zur Durchführung der erforderlichen Kurvenangleichungsfunktion, sobald die Rohdaten erhalten wurden. Eines dieser Programme ist HyperFit, das als Freeware-Demoversion (eingeschränkte Funktionalität) und als lizenzierte Version verfügbar ist. Eine vollständige Lizenz ist erforderlich, um die Kurve und die resultierenden Materialkonstanten zu generieren.
Das hyperelastische Mooney-Rivlin-Materialmodell
Hyperelastische Materialien in Fusion werden mithilfe des Mooney-Rivlin-Materialmodells (Standard mit zwei Konstanten) modelliert. Da die Formel für das nahezu nicht kompressible Verhalten verwendet wird, werden volumetrische Formeln in die Dehnungsenergiefunktion eingeschlossen. Die Effekte der Scherverzerrung und der volumetrischen Verformung werden getrennt.
Allgemeine Mooney-Rivlin-Dehnungsenergie-Funktion
Die Beziehung zwischen der Dehnungsenergie, der Scherverzerrung und der volumetrischen Verformung wird mit der folgenden allgemeinen Fallfunktion (gültig für Fälle mit zwei oder mehr Konstanten) angegeben:
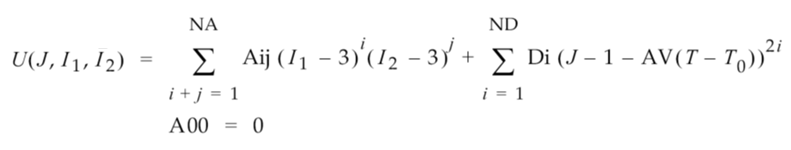
Dabei gilt:
- U ist die Dehnungsenergie.
- I1 ist die erste distortionale Dehnungsinvariante.
- I2 ist die zweite distortionale Dehnungsinvariante.
- J = det F ist die Determinante des Verformungsgradienten.
- Aij ist die Materialkonstante der Scherverzerrung (dabei sind i und j die tiefgestellten Indizes der einzelnen Konstanten).
- Di ist die Materialkonstante der volumetrischen Verformung.
- AV ist der volumetrische Wärmeausdehnungskoeffizient.
- T ist die aktuelle Temperatur.
- T0 ist die Ausgangstemperatur
Vereinfachte Mooney-Rivlin-Gleichung mit zwei Konstanten
Aktuell unterstützt Fusion keine thermischen Effekte für hyperelastische Materialien in nichtlinearen Analysen. Daher können wir die vorherige Funktion vereinfachen, indem die Formeln für die thermische Ausdehnung (AV, T und T0) gestrichen werden, und indem wir die Summierung für die Konstanten berechnen, die Fusion akzeptiert (A01, A10 und D1). Die vereinfachte Gleichung für die Dehnungsenergie lautet dann wie folgt:
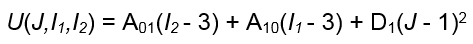
Dabei gilt:
- *U, J, I1* und I2 bleiben wie zuvor definiert.
- A01 ist die erste von zwei distortionalen Konstanten für die Scherverformung des Materials.
- A10 ist die zweite von zwei distortionalen Konstanten für die Scherverformung des Materials.
- D1 ist die Konstante für die volumetrische Verformung des Materials, wobei diese der Hälfte des Massenmoduls (K) entspricht.
Das bedeutet 2D1 = K. Und damit D1 = K/2