Theoretischer Hintergrund zu modalen Frequenzen

Der mathematische Prozess für die Bestimmung von Eigenfrequenzen und den entsprechenden Modusformen mittels der Finite-Elemente-Methode ist komplex. Damit die Theorie leichter verständlich ist, verwenden wir ein sehr einfaches lineares Feder-Masse-System mit einem Freiheitsgrad (FHG). Das bedeutet, dass sich die Masse nur in einer Richtung bewegen kann.

In der folgenden Abbildung ist m die Masse, und k ist die Steifigkeit der Feder:

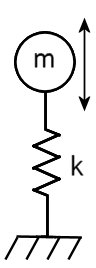
Freiheitsgrade Feder-Masse-System - Diagramm

Das Hookesche Gesetz definiert die Kraft (F), die zur Auslenkung einer Feder der Steifigkeit (k) um eine Distanz (X) erforderlich ist, wie folgt:

(1) F = k·X

Das zweite Newtonsche Gesetz der Bewegung gibt das Verhältnis zwischen Kraft (F), Masse (m) und Beschleunigung (a) für das System mit einem einzelnen Freiheitsgrad wie folgt an:

(2) F = m·a

Die Kombination dieser beiden Gleichungen ergibt eine Beziehung zwischen der Masse (m), Beschleunigung (a), Federsteifigkeit (k) und Auslenkung (X):

(3) m·a = k·X

Die folgende Gleichung liefert die Winkelfrequenz der Schwingung (ω) in Radiant pro Sekunde für dieses einfache lineare Feder-Masse-System:

(4) ω = (k/m)1/2

Es gibt 2π Radiant pro Schwingungszyklus. Somit liefert die nächste Gleichung die Eigenfrequenz der Schwingung (fn) in Hertz:

(5) fn = (k/m)1/2 / (2·π)

In einem realen Finite-Elemente-Modell gibt es 3D-Bewegung und viele Freiheitsgrade aufgrund all der Knoten und Elemente im Netz.

Anmerkung: Wir berücksichtigen die Dämpfung bei der Berechnung der Eigenfrequenz nicht. Dämpfung wird als Verringerung der Schwingungsamplitude aufgrund des Abführens von Energie aus dem System definiert. Energie geht infolge von Reibung, Viskosität oder anderen Widerstandskräften verloren. Die Menge an Dämpfung in typischen Fertigungsmaterialien (wie Stahl, Aluminium und Beton) ist gering. Deswegen unterscheidet sich die Eigenfrequenz ohne Dämpfung in der Regel nicht sehr von der tatsächlichen Eigenfrequenz. Dämpfung verringert die Schwingungsfrequenz in Bezug auf ein ungedämpftes System.

In einem kontinuierlichen System gibt es eine unbegrenzte Anzahl an Schwingungsmodi. In einem Finite-Elemente-Modell gibt es jedoch nur eine begrenzte Anzahl an Freiheitsgraden und infolgedessen eine begrenzte Anzahl an Schwingungsmodi. Die Bestimmung der Schwingungsfrequenzen und Modusformen für diese komplexen 3D-Systeme umfasst Matrizenoperationen, Eigenwerte und Eigenvektoren.

Die Gleichung (4) stellt ein Eigenwert-Eigenvektor-Problem mit einer begrenzten Anzahl von Lösungen dar. Die Winkelfrequenz (ω) ist eine skalare Menge. Bei einer bestimmten Lösung oszillieren alle Freiheitsgrade mit der gleichen Winkelfrequenz. Die Amplitude der Schwingung (δ) ist jedoch eine Vektorgröße. In unserem komplexen System entspricht δ der Verschiebung (X) im Beispiel mit dem einzelnen Freiheitsgrad. Die verschiedenen Freiheitsgrade oszillieren mit unterschiedlichen Amplituden, angegeben durch die Komponenten von δ. Diese Amplitudenvariation liefert die Modusform.

Eine genaue Definition der Eigenwerte und Eigenvektoren und der mathematischen Operationen, die zur Lösung einer Modalanalyse verwendet werden, würde über den Rahmen dieses Themas hinausgehen.